2015-08-13
9894
Если вопрос о приводимости и неприводимости многочленов над полем C и R решается легко, то вопрос о приводимости и неприводимости многочленов над полем Q решается довольно сложно.
Существует несколько достаточных критериев приводимости и неприводимости многочленов и несколько необходимых. Мы рассмотрим наиболее важные.
Если многочлен 
с целыми коэффициентами имеет рациональный корень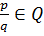 
, то он приводим над Q 
.
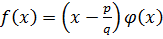Докажем критерий Эйзенштейна (достаточное условие того, чтобы многочлен с целыми коэффициентами был неприводим над Q).
Многочлен с целыми коэффициентами
, 
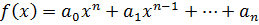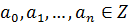
будет неприводим над Q, если существует простое число p, удовлетворяющее условиям:
1) 
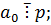
2) 
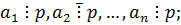
3) 
.
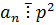Доказательство:
Пусть удовлетворяет всем условиям критерия и пусть он приводим =>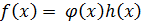 
.
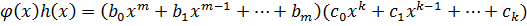, где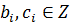 
.
Тогда
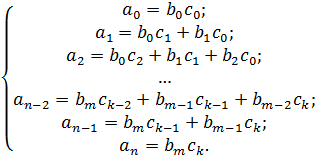
Все коэффициенты, кроме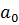 
делятся на p, когда 
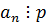, но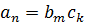 
, 
.
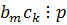Пусть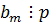 
(если бы 
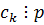, то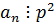 
, а у нас 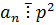, значит 
).
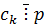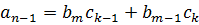, тогда 
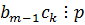, но =>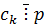 
.
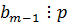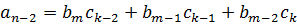, тогда 
=> 
.
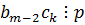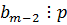На m-ом шаге получим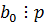 
. Поднимемся в первое равенство:
=> 
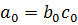, а это против условия (1) критерия Эйзенштейна.
Значит многочлен неприводим.
Пример: Выяснить приводимость многочлена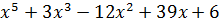 
существует 3: 
.
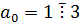0,3,-12,39,6 
3. Значит многочлен неприводим над Q.
Из критерия Эйзенштейна следует, что над полем Q существует неприводимый многочлен сколь угодно большой степени. Докажем, что существует многочлен тысячной степени.
.
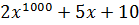2 
5;
0,…,0,5,10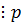 
.
10 25.
Значит многочлен неприводимый над полем Q.
Критерия Эйзенштейна является лишь достаточным условием, поэтому если хотя бы одно из условий критерия не выполняется, то о многочлене нельзя сказать приводимый он или неприводимый.
