Многочлен вида
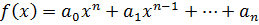 ,
, 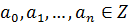
называется примитивным, если его коэффициенты взаимно простые числа
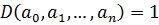 .
.
Например: 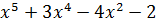 - примитивный.
- примитивный.
Теорема: Всякий многочлен с рациональными коэффициентами можно представить в виде произведения несократимой дроби на примитивный многочлен.
Доказательство:
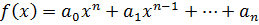 ,
, 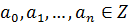 .
.
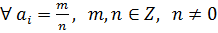 .
.
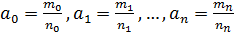 .
.
Найдется 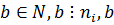 - общий знаменатель.
- общий знаменатель.
По свойству дробей все коэффициенты можно привести к общему знаменателю 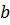 .
.
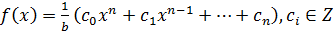 .
.
 .
.
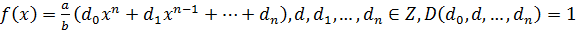 - примитивный многочлен.
- примитивный многочлен.
Если  – несократимая, то теорема доказана.
– несократимая, то теорема доказана.
Если  - сократимая, то
- сократимая, то 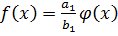 ,
,  – примитивный.
– примитивный.
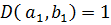 . Ч.т.д.
. Ч.т.д.
Например: 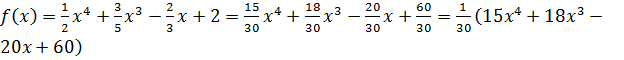 .
.
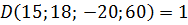 .
.
Лемма Гаусса: Произведение примитивных многочленов является примитивным.
Доказательство:
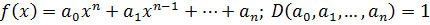 .
.
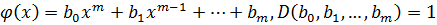 .
.
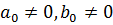 .
.
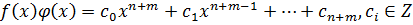 .
.
Предположим, что этот многочлен не примитивный. Тогда 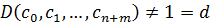 .
.
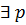 - простое число, на которое все коэффициенты делятся.
- простое число, на которое все коэффициенты делятся.
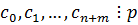 .
.
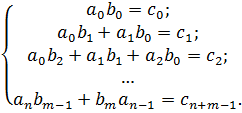
Т.к. многочлены 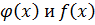 являются примитивными, то все коэффициенты и первого, и второго многочлена делиться на p не могут.
являются примитивными, то все коэффициенты и первого, и второго многочлена делиться на p не могут.
Пусть 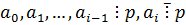 .
.
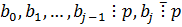 .
.
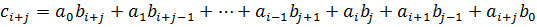 .
.
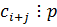 по условию все слагаемые, кроме одного делятся на p. Тогда
по условию все слагаемые, кроме одного делятся на p. Тогда 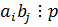 , отсюда
, отсюда 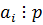 или
или 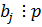 , а это противоречит выбору коэффициентов
, а это противоречит выбору коэффициентов 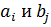 . Противоречие в результате неверного предположения. Значит
. Противоречие в результате неверного предположения. Значит 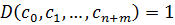 . Значит многочлены
. Значит многочлены 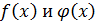 – примитивные.
– примитивные.
 2015-08-13
2015-08-13 2757
2757








