Пусть многочлен  с рациональными коэффициентами. Тогда его можно представить как
с рациональными коэффициентами. Тогда его можно представить как 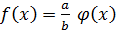 ,
,  – примитивный,
– примитивный,  – несократимая дробь.
– несократимая дробь.
Если  с целыми коэффициентами будет приводим над Z:
с целыми коэффициентами будет приводим над Z:
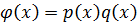 ,
, 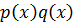 с целыми коэффициентами, ст.
с целыми коэффициентами, ст. 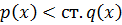 , ст.
, ст. 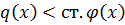 ,
,
тогда 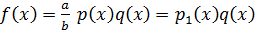 ,
,  - приводим.
- приводим.
Пусть  приводим над Q. Тогда покажем, что он приводим над кольцом Z.
приводим над Q. Тогда покажем, что он приводим над кольцом Z.
Пусть 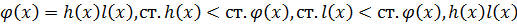 с рациональными коэффициентами.
с рациональными коэффициентами.
Тогда 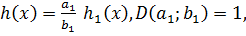
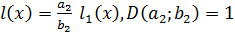 .
.
Тогда 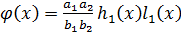 .
.
По лемме Гаусса 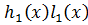 – примитивные его коэффициенты целого и взаимно простые,
– примитивные его коэффициенты целого и взаимно простые,  - примитивный с целыми и взаимно простыми коэффициентами.
- примитивный с целыми и взаимно простыми коэффициентами.
Тогда 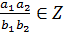 .
.
Произведение примитивно умноженного на 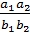 даст нам многочлен с целыми коэффициентами ó
даст нам многочлен с целыми коэффициентами ó 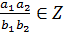 .
.
А значит 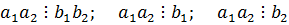 .
.
Т.к. 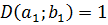 , то
, то 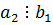 ,
, 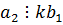 .
.
Т.к. 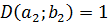 , то
, то 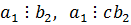 .
.
Получили 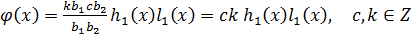 .
.
Разложили  ,
,  приводим над Z. Значит
приводим над Z. Значит  будет приводим над Q.
будет приводим над Q.
Вопрос о приводимости многочлена над Q сводится к вопросу о приводимости над Z.
 2015-08-13
2015-08-13 1429
1429








