Пусть P – произвольное числовое поле.
x 1, x 2, …, x n – переменные.
Выражение вида 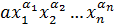 (1), где
(1), где 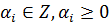 называется одночленом от n переменных, a – коэффициент одночлена.
называется одночленом от n переменных, a – коэффициент одночлена.
Конечная сумма одночленов от n переменных называется многочленом от n переменных.
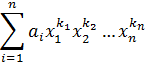
Степенью одночлена (1) относительно всех переменных называется число равное сумме показателей (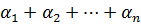 ).
).
Каждый член многочлена имеет свою степень.
Степенью многочлена от n переменных относительно всех переменных называется наибольшая из степеней членов данного многочлена.
Множество всех многочленов от n переменных 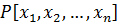 .
.
Теорема: Множество всех многочленов от n переменных над полем P является кольцом.
Введем операцию сложения.
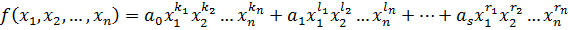 . (1)
. (1)
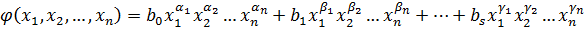 . (2)
. (2)
Два одночлена называются подобными, если они различаются только числовым коэффициентом.
В записи (1) и (2) многочлена не должно быть подобных.
Суммой двух многочленов 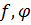 назовем новый многочлен, который получается при приписывании членам первого многочлена всех членов второго многочлена с теми же знаками.
назовем новый многочлен, который получается при приписывании членам первого многочлена всех членов второго многочлена с теми же знаками.
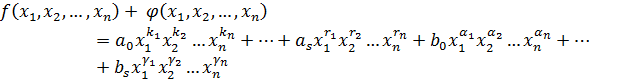
Из определения суммы двух многочленов следует, что сложение многочленов коммутативно и ассоциативно.
Роль нуля при сложении многочленов играет нулевой многочлен 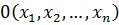 .
.
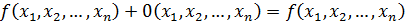
Для любого многочлена существует ему противоположный.
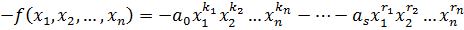
По сложению многочлены образуют абелеву группу.
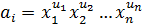
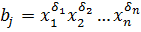
Произведением двух одночленов назовем выражение вида
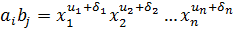
Произведение двух многочленов от n переменных называется новый многочлен, который получается в результате последовательного перемножения всех членов первого на все члены второго многочлена и приведения подобных одночленов.
Нетрудно доказать, что умножение многочленов дистрибутивно относительно сложения.
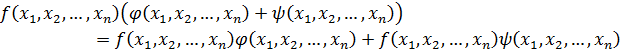
Мы доказали, что множество всех многочленов является кольцом (коммутативное, ассоциативное, 0-ой элемент, 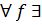 противоположный, умножение дистрибутивно).
противоположный, умножение дистрибутивно).
Кольцо коммутативно-ассоциативное с 1.
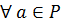 – многочлен нулевой степени
– многочлен нулевой степени
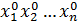
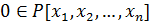 .
.
 2015-08-13
2015-08-13 3192
3192








