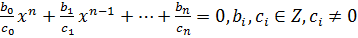2015-08-13
3520
. (1)
Если умножить на общий знаменатель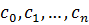 
, то получим уравнение с целыми коэффициентами
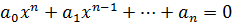. (2)
Если α – корень 1 => α - корень 2.
Если α – корень 2 => α - корень 1.
Сведется к нахождению корней уравнения с целыми коэффициентами.
Теорема 1: Если несократимая дробь 
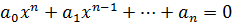является корнем уравнения (2), 
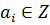, то числитель дроби – p является делителем свободного члена an, а q является положительным делителем старшего коэффициента.
Доказательство:
Дано: - корень уравнения (2) => 
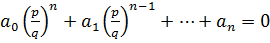- верное равенство. Умножим его на qn.
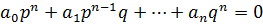
Все слагаемые от 1-го до предпоследнего делятся на p; сумма делится на p => последнее слагаемое делится нацело на p -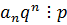 
.
Все слагаемые, кроме 1-го, делятся на q и сумма делится нацело на q =>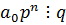 
.
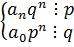
Т.к. p, q – взаимно-простые, то любая степень q с числом p взаимно-простые и наоборот.
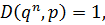
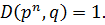
По теореме о взаимно-простых числах (если произведение на число, а один из сомножителей взаимно-простое с этим числом => второе слагаемое делится нацело на p)
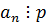
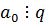
p – делитель свободного члена,
q – делитель старшего коэффициента.
|
|
|
Учитывая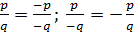 
, знаменатель можно брать положительный.
Следствие 1: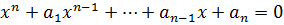 
. Если старший коэффициент равен 1, то его корнями могут быть только целые числа, являющиеся делителями свободного числа.
Доказательство:
Если является корнем уравнения, то по предшествующей теореме q – делитель старшего коэффициента, q – делитель 1.
Значит делитель будет p – делитель свободного члена.
Следствие 2: Целыми корнями уравнения 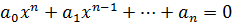могут быть делители свободного члена.
Доказательство:
По теореме, если – корень уравнения (2), то p является делителем свободного члена; q – положительный делитель старшего коэффициента.
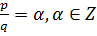только тогда, когда p=α, q=1 => α является делителем свободного члена.
Теорема является необходимым условием того, чтобы рациональное число было корнем многочлена с целыми коэффициентами.
1-е необходимое условие существования рационального корня у многочлена с целыми коэффициентами:
Для того чтобы несократимая дробь была корнем уравнения (2) с целыми коэффициентами необходимо, чтобы числитель этой дроби был делителем свободного члена, а знаменатель – положительным делителем старшего коэффициента.
Пример: 3 x 4+5 x 3+ x 2+5 x -2=0
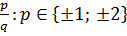- делители.
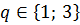
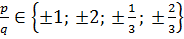эти числа могут быть рациональными корнями.
| -2 | |||||
| -2 | -1 | -1 | |||
| 1/3 |
-2; 1/3.
Замечание: Если дробей вида будет много, то существует второе необходимое условие.
Теорема 2: Если – несократимая дробь является корнем уравнения (2) с целыми коэффициентами ,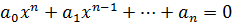 
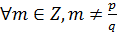, то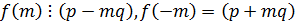 
.
Доказательство:
Дано: - корень.
Тогда по критерию существования корня
| 
| 
| … | 
| 
| |
|
| 
| 
| … | ||
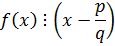
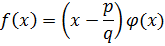
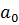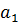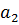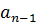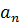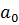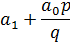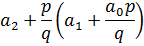| q0 | q1 | q2 |
Найдем коэффициенты частного.
|
|
|
Коэффициенты частного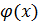 
будут дроби со знаменателями q0, q1, …, qn-1.
,
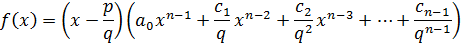
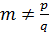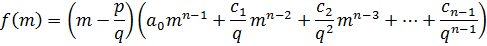
Обе части умножим на qn.
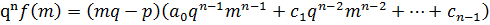
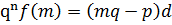
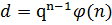– целое число.
Т.к.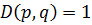 
, то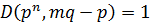 
.
.
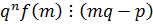ð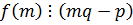 
=> 
.
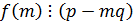Если вместо m подставить –m, то аналогично получим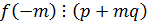 
. Ч.т.д.
2-е необходимое условие:
Для того чтобы несократимая дробь являлась корнем многочлена с целыми коэффициентами необходимо, чтобы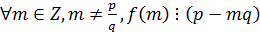 
, .
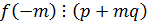Замечание: На практике в качестве m берут ±1.
Пример: Найти рациональные корни многочлена.
3 x 5+17 x 4+36 x 3+38 x2 +19 x +5
.
.
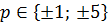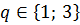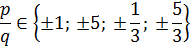
f(1)=118
f(-1)=0
| p | -5 | -1 | -5 |
| q |
.
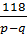| -1 | ||||||
| -1/3 | ||||||
| -5/3 |
Рациональных корней нет.
