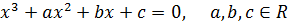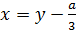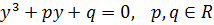Уравнения третьей степени с действительными коэффициентами

.

.

. (2)

.

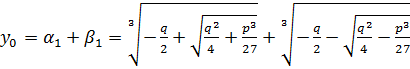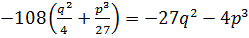–называется дискриминантом кубического уравнения (2).

1) D<0 => .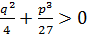

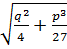- положительное действительное число.

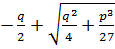- действительное число.

.

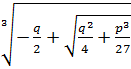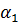– действительное, 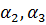- комплексно-сопряженные.

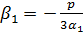– действительное, 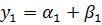– действительное.

.

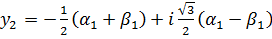Один действительный корень и два комплексно-сопряженных.

2) D=0 => .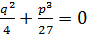

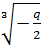- действительное число.

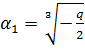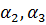, - комплексно-сопряженные.

.

.

.

.

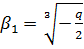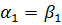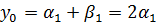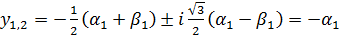Все три корня действительные числа.

3) D>0 => .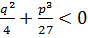

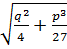– линейное число.

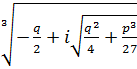- комплексное число.

Корень третьей степени отличается от действительного. Действительным быть не может.

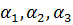– комплексные числа.

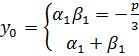– действительные корни <=> когда числа являются комплексно-сопряженными .

;

.

.

.

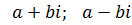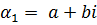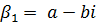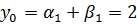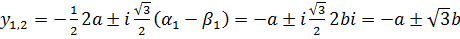Все три корня действительные числа.

Корни кубического уравнения часто находят приближенным методом.