Однородные многочлены. Степень произведения многочленов

Многочлен от n переменных 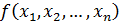называется однородным, если все его члены имеют одинаковую степень.

Однородные многочлены называют формой m-ой степени.

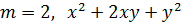однородный многочлен 2-ой степени.

Теорема: Всякий многочлен от n переменных можно представить в виде суммы нескольких однородных многочленов.

Доказательство:

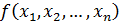найдем наибольшую степень одночлена, членов имеющих наибольшую степень может оказаться несколько.

Соберем все члены, имеющие наибольшую степень.

Из оставшихся многочленов выберем одночлен, имеющий наибольшую одинаковую степень. И т.д.

;

;

… .

.

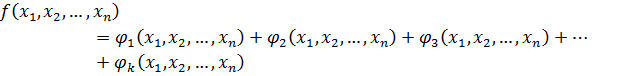
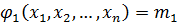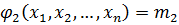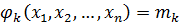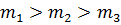Мы записали многочлен в виде суммы одночленов.

Теорема: Степень произведения двух многочленов равна сумме степеней сомножителей.

Доказательство:

, .

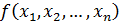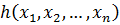Ст. f=m.

Ст. h=k.

Ст. f·h=m+k.

Многочлены f и h представим в виде суммы однородных многочленов.

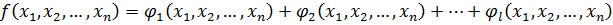
Ст. .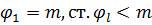

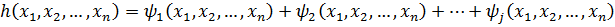
Ст. .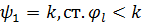

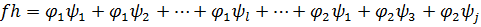
Однородный многочлен ст. 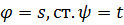, s+t.

В произведении f·h все слагаемые будут однородными одночленами, причем ст. 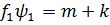, а степени всех остальных слагаемых <m+k.

Ст. f·h=m+k.

Если f и h ненулевые, то их произведение ненулевым многочленом не будет.

Кольцо многочленов не содержит делителей нуля.