Приведемо це рівняння до вигляду (2.2):
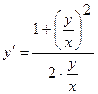 .
.
Замінимо: 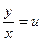 ,
, 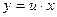 ,
, 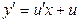 .
.
Отримаємо рівняння: 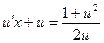 ;
; 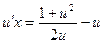 ;
; 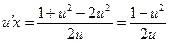 ;
;
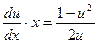 ;
; 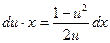 ;
; 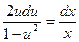 .
.
Проінтегруємо: 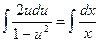 .
.
Маємо: 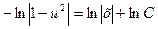 . (Якщо при розв’язуванні отримано логарифми, зручно подати довільну сталу інтегрування С у вигляді логарифма
. (Якщо при розв’язуванні отримано логарифми, зручно подати довільну сталу інтегрування С у вигляді логарифма 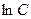 ).
).
Звідки: 
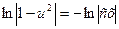 ,
, 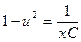 .
.
Повертаємось до вихідних змінних: 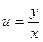 , тоді:
, тоді:
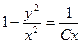 ;
; 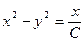 ;
; 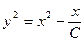 ;
; 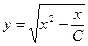 .
.
Відповідь: 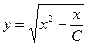 .
.
Зауваження: Приклад 4 – зразок розв’язання завдання № 2.
2.3. Лінійні диференціальні рівняння.
Означення 5. Лінійним диференціальним рівнянням називається рівняння, що має вигляд: 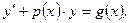 (2.4)
(2.4)
де 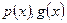 – функції, які залежать тільки від змінної х.
– функції, які залежать тільки від змінної х.
Метод розв’язання: робимо заміну невідомої функції: 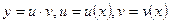 – деякі невідомі функції. Тоді
– деякі невідомі функції. Тоді 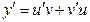 .
.
Після заміни в рівнянні (2.4) маємо:
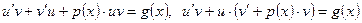
Далі виконуємо штучний крок: вважаємо невідому функцію v такою, що вираз у дужках (який завжди є множником до u та містить v и v /) має дорівнювати нулю:
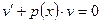 . (2.5)
. (2.5)
Враховуючи це, маємо, що для функції u виконується рівність:
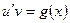 . (2.6)
. (2.6)
З рівностей (2.5) і (2.6) знаходимо функції 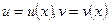 .
.
 2015-08-13
2015-08-13 277
277








