Розв’язання

Функцію перед dx не можна розкласти на множники, кожен з яких залежить тільки від однієї змінної х або у. Тому приклад 3 не можна розв’язати як рівняння із змінними, що розділяються.

Приведемо дане рівняння до вигляду (2.2). Перенесемо доданок у праву частину рівняння: .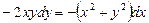

Поділимо на 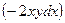ліву та праву частини рівняння:

.

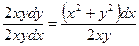Після скорочення маємо: .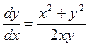

Замінимо: 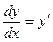. Чисельник та знаменник дробу справа поділимо на 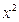. При цьому дріб не зміниться.

= , = .

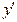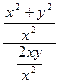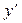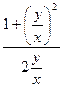У правій частині отримали функцію, залежну тільки від 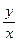, тобто функцію, яку в загальному вигляді можна записати: f .

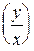Метод розв’язання: робимо заміну 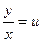. Тоді 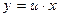. Знайдемо 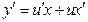, а, оскільки 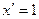, то 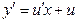. У результаті маємо рівняння зі змінними, що розділяються.