2015-08-13
270
Розв’язати рівняння: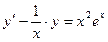 
.
Розв’язання
Виконавши заміну: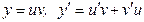 
, маємо:
.
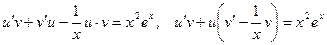1. 
, 
,
,
.
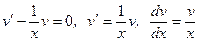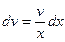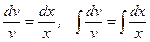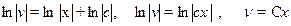На цьому етапі довільну сталу С замінимо зручним значенням С= 1 (в інших випадках С= 0). Отже, v = x.
2. 
.
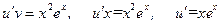
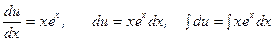а)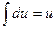 
;
б)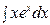 
– інтегруємо за частинами, використовуючи формулу:
.
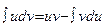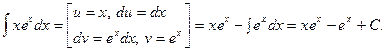
Таким чином,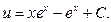 
3. Шукана функція: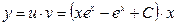 
Відповідь: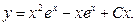 
Зауваження: приклад 5 – зразок розв’язання завдання №3.
Диференціальні рівняння другого порядку
3.1. Рівняння вигляду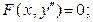 
Якщо з рівняння можна виділити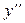 
як функцію, залежну тільки від х, тобто 
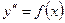, то розв’язок у=у (х) знаходимо, інтегруючи ліву та праву частини рівняння двічі.
