Частинні похідні 1-го порядку функції кількох змінних.Необхідна і достатня умова диференційованості функції двох змінних.
Крім повного приросту ФДЗ
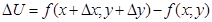 ,
,
існують частинні прирости:
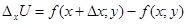 ,
,
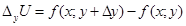 .
.
Означення. Якщо існує границя відношення частинного приросту ФДЗ до приросту відповідного аргументу, коли останній прямує до нуля, то його називають частинноюпохідною й позначають:
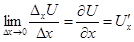 ,
,
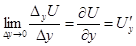 .
.
Зауваження. Частинну похідну 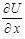 обчислюють як похідну функції однієї змінної за умови, що y зафіксовано, аналогічно для
обчислюють як похідну функції однієї змінної за умови, що y зафіксовано, аналогічно для 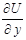 - x зафіксовано.
- x зафіксовано.
Локальні екстремуми функцій двох змінних.Дослідження функцій двох змінних на екстремум.
Локальні екстремуми функції двох змінних
Нехай функція z = f(х, у) визначена в області D, а точка 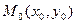
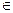 D. Якщо існує окіл точки
D. Якщо існує окіл точки 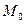 , який належить області D і для всіх відмінних від
, який належить області D і для всіх відмінних від 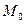 точок М цього околу виконується нерівність f (М)< f (
точок М цього околу виконується нерівність f (М)< f (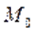 )(f (М) > f (
)(f (М) > f (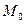 )), то точку
)), то точку 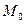 називають точкою локального максимуму (мінімуму) функції
називають точкою локального максимуму (мінімуму) функції 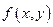 , а число
, а число 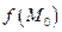 – локальним максимумом (мінімумом) цієї функції.
– локальним максимумом (мінімумом) цієї функції.
Точки максимуму та мінімуму функції називають її точками екстремуму.
|
|
|
Необхідна ознака існування екстремуму
Якщо функція 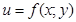 набуває у точці
набуває у точці 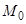 свого екстремального значення, то
свого екстремального значення, то 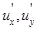 в точці
в точці 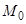 або дорівнюють нулю, або нескінченності, або не існують.
або дорівнюють нулю, або нескінченності, або не існують.
Доведення
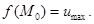 Крива
Крива 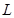 - лінія перетину поверхні
- лінія перетину поверхні 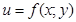 й площини
й площини 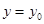 , тоді
, тоді 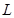 задана рівнянням
задана рівнянням 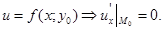 Аналогічно доводиться, що
Аналогічно доводиться, що 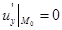 й ін. випадки.
й ін. випадки.
Достатня ознака існування екстремуму
Теорема. Нехай у 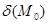 функція
функція 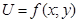 має неперервні частинні похідні до 3-го порядку включно і точка
має неперервні частинні похідні до 3-го порядку включно і точка 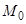 є стаціонарною, тоді:
є стаціонарною, тоді:
1) при 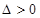 є екстремум, якщо
є екстремум, якщо 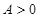 , то в точці
, то в точці 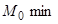 , якщо
, якщо 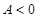 ,то в точці
,то в точці 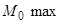 ;
;
2) при 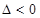 - екстремуму немає;
- екстремуму немає;
3) при 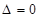 - потрібні додаткові дослідження.
- потрібні додаткові дослідження.
Тут 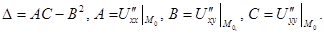
 2015-08-13
2015-08-13 1994
1994







