Невласні інтеграли 1 та 2 роду

За теоремою про існування визначеного інтеграла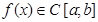

1.

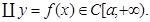
Означення. 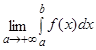називають невласним інтегралом 1-го роду й позначають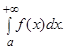

Аналогічно визначаються через границі такі невласні інтеграли:

;

.

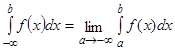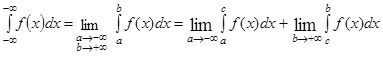Якщо границя в невласному інтегралі дорівнює скінченному числу, то інтеграл називається збіжним, у протилежному разі – розбіжним.

2. 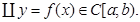і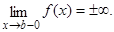

Означення. 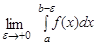називають невласним інтегралом 2-го роду й позначають .

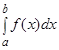Інтеграл збігається, якщо границя дорівнює скінченному числу й розбігається, якщо він дорівнює нескінченності або не існує. Аналогічно визначаються невласні інтеграли, коли 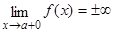або в точці 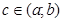неусувний розрив 2-го роду:

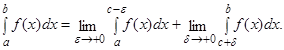
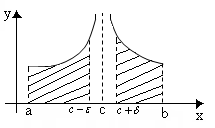
Зауваження. В останньому випадку, якщо хоча б одина з границь дорівнює нескінченності або не існує, то 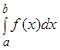розбігається.