Кратні інтеграли та їх застосування

Означення подвійного інтеграла циліндричний координата

Нехай функція 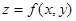визначена в обмеженій замкнутій області 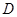площини 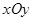. Розіб’ємо область 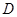довільним чином на 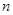елементарних областей, площі котрих, як і самі області, позначатимемо 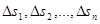. У кожній елементарній області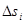 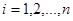виберемо довільну точку .

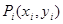Подвійним інтегралом від функції 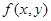по області 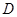називається границя інтегральної суми (1) за умови, що найбільший із діаметрів 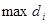, 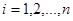прямує до нуля:

.

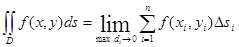Подвійний інтеграл позначають так:

.

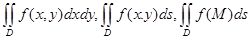Означення потрійного інтеграла

Нехай функція 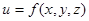визначена в замкненій обмеженій області 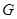тривимірного простору 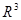. Розіб’ємо область 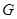на 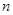довільних частинних областей 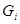, які не мають спільних внутрішніх точок. Об’єми областей 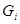позначимо позначимо 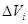, їх діаметри -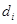 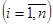. Діаметром 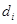області 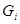називається довжина найбільшої хорди, яка з’єднує дві точки межі області 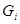. Візьмемо довільну точку 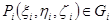, і знайдемо значення функції 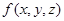у точці .

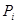Вираз вигляду 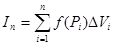називається інтегральною сумою для функції 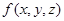по області 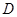. Позначимо через 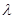максимальний із діаметрів 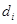областей 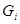, тобто , .

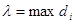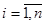Якщо існує границя інтегральної суми 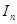за умови, що 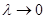, тобто 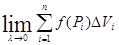, яка не залежить від способу розбиття області 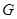а елементарні області 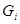та від вибору точок 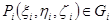, то ця границя називається потрійним інтегралом від функції 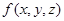по області 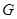. Потрійний інтеграл позначається так:

.

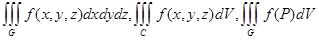Застосовується у механіці та фізиці.Наприклад у задачах вимірювання маси,обчислення статичних моментів,моменту інерції