Матрица любого бинарного отношения обладает следующими свойствами:
1. Если 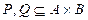 и
и 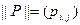 ,
, 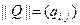 , то
, то 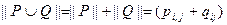 ;
; 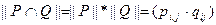 , причем сложение элементов определяется по правилам: 0+0=0; 1+0=0+1=1; 1+1=1, а умножение – почленно обычным образом, то есть по правилам: 1*0=0*1=0; 1*1=1; 0*0=0.
, причем сложение элементов определяется по правилам: 0+0=0; 1+0=0+1=1; 1+1=1, а умножение – почленно обычным образом, то есть по правилам: 1*0=0*1=0; 1*1=1; 0*0=0.
2. Если 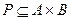 ,
, 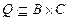 , то
, то 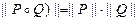 и матрицы умножаются по обычному правилу умножения матриц, но произведение и сумма элементов при перемножении матриц находится по правилам п.1.
и матрицы умножаются по обычному правилу умножения матриц, но произведение и сумма элементов при перемножении матриц находится по правилам п.1.
3. 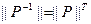 , где
, где 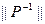 - матрица обратного отношения
- матрица обратного отношения 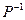 .
.
4. Если 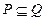 , то
, то 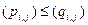 , где
, где 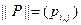 ,
, 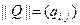 .
.
Пример 4. Пусть 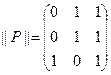 ,
, 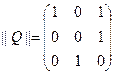 .
.
 2015-08-12
2015-08-12 479
479








