Определение свойств бинарного отношения по его матрице

1. Главная диагональ матрицы рефлексивного отношения P всегда состоит из одних единиц, так как 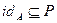, если .

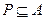P рефлексивно тогда и только тогда, когда главная диагональ матрицы || P || со- держит только единицы.

2. P – симметрично, тогда и только тогда, когда .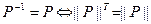

P симметрично тогда и только тогда, когда матрица симметрична относительно главной диагонали.

3. P – антисимметрично, тогда и только тогда, когда 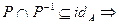в матрице 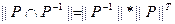все элементы вне главной диагонали являются нулевыми.

P антисимметрично тогда и только тогда, когда матрица 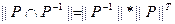вне главной диагонали содержит только нули.

4. P – транзитивно, тогда и только тогда, когда .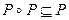

P транзитивно тогда и только тогда, когда 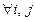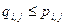, где , .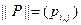

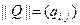Пример 12. Пусть , , , .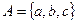

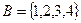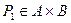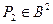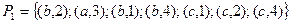
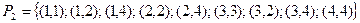
Изобразить графы отношени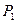й и 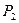, найти матрицу 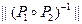. Проверить с помощью матрицы 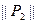, является ли отношение 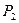рефлексивным, симметричным, транзитивным.