2015-08-12
365
Следствие. Пусть R – отношение эквивалентности на множестве А, тогда
1) (
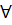
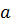Î А) Α Î 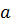/R.
2) 
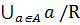= A.
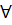
3) ( 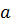,b Î А) 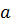/R = b/R Û 
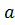R b.
4) 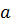/R ≠ b/R Û 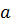/R ∩ b/R = Æ.
Пусть S – разбиение непустого множества А и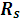 
- бинарное отношение, определяемое следующим образом: (x,y) Î 
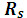тогда и только, когда x и y принадлежат одному и тому же подмножеству семейства S.
Теорема 3. (обратная теореме 1). Отношение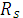 
соответствующее разбиению S непустого множества А, является отношением эквивалентности на А, причём фактор- множество А/ 
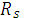совпадает с разбиением S.
