Теоретический материал

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

F(x) + C. Записывают: 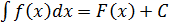, где 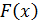- есть некоторая первообразная функции 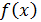на этом промежутке, С – const. При этом знак 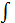называется знаком интеграла, 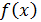- подынтегральной функцией, 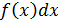- подынтегральным выражением, 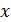- переменная интегрирования, С- постоянная интегрирования.

Операция нахождения неопределенного интеграла от данной функции называется интегрированием данной функции.

Интегрирование – операция, обратная операции дифференцирования. У всякой непрерывной на данном интервале функции существует неопределенный интеграл.

Таблица неопределенных интегралов

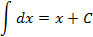
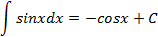
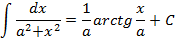
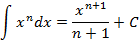
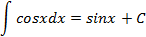
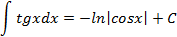
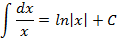
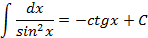
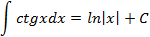
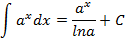
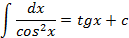
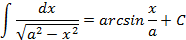
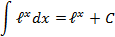
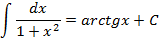
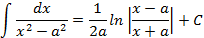
Свойства неопределенного интеграла:

;

;

;

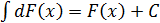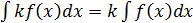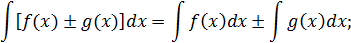
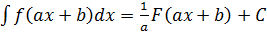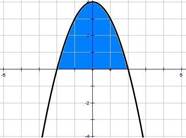Определение: Фигура, ограниченная снизу отрезком [a, b] оси Ох,сверху графиком непрерывной функции у= f(x), принимающей положительные значения, а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.

.

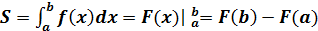Образец решения:

Вычислить площадь криволинейной трапеции, ограниченной линиями

у = 4 - х² и у=0

Решение:

1. у = 4 - х ² - квадратичная функция, график – парабола, ветви направлены вниз, вершина (0;4)
у = 0 - ось абсцисс.

2. Найдём точки пересечения параболы с осью Х: ;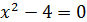

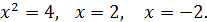
3. Найдём площадь криволинейной трапеции по формуле:

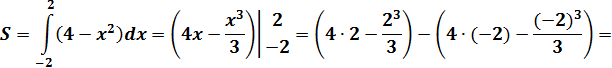
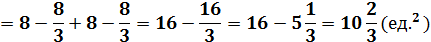
Решить самостоятельно:

Вариант 1

1. Найти площадь фигуры, ограниченной линиями:

1.1 .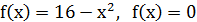

1.2. .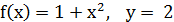

1.3. .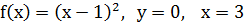

1.4. .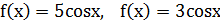

1.5. .

Вариант 2

1. Найти площадь фигуры, ограниченной линиями:

1.1. .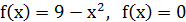

1.2.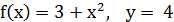

1.3. .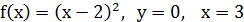

1.4. .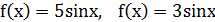

1.5. .