Пусть задана зависимость двух переменных 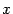 и
и 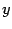 от параметра
от параметра 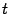 , изменяющегося в пределах от
, изменяющегося в пределах от 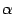 до
до 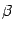 :
:
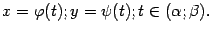
Пусть функция 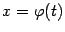 имеет обратную:
имеет обратную: 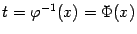 . Тогда мы можем, взяв композицию функций
. Тогда мы можем, взяв композицию функций 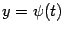 и
и 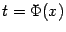 , получить зависимость
, получить зависимость 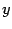 от
от 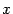 :
: 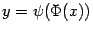 . Зависимость величины
. Зависимость величины 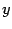 от величины
от величины 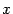 , заданная через зависимость каждой из них от параметра
, заданная через зависимость каждой из них от параметра 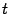 в виде
в виде 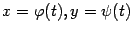 , называется функцией
, называется функцией 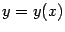 , заданной параметрически.
, заданной параметрически.
Производную функции 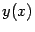 , заданной параметрически, можно выразить через производные функций
, заданной параметрически, можно выразить через производные функций 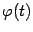 и
и 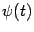 : поскольку
: поскольку 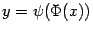 и, по формуле производной обратной функции,
и, по формуле производной обратной функции, 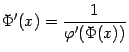 , то
, то
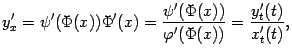
где 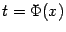 -- значение параметра, при котором получается интересующее нас при вычислении производной значение
-- значение параметра, при котором получается интересующее нас при вычислении производной значение 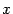 .
.
Заметим, что применение формулы приводит нас к зависимости между 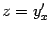 и
и 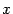 , снова выраженной в виде параметрической зависимости:
, снова выраженной в виде параметрической зависимости: 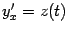 ,
, 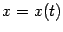 ; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции
; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции 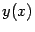 . Несмотря на то, что производная не выражена через
. Несмотря на то, что производная не выражена через 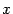 в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра
в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра 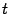 . Покажем это на следующем примере.
. Покажем это на следующем примере.
Пример 4.22 Пусть зависимость между 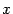 и
и 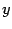 задана параметрически следующими формулами:
задана параметрически следующими формулами:
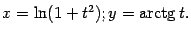
Найдём уравнение касательной к графику зависимости 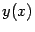 в точке
в точке 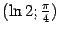 .
.
Значения 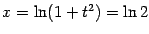 и
и 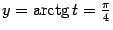 получаются, если взять
получаются, если взять 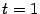 . Найдём производные
. Найдём производные 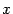 и
и 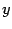 по параметру
по параметру 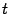 :
:
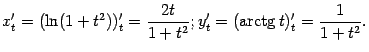
Поэтому
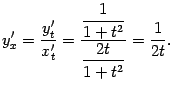
При 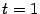 получаем значение производной
получаем значение производной
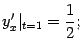
это значение задаёт угловой коэффициент 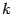 искомой касательной. Координаты
искомой касательной. Координаты 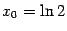 и
и 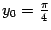 точки касания заданы в условии задачи. Значит, уравнение касательной таково:
точки касания заданы в условии задачи. Значит, уравнение касательной таково:
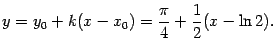
Заметим, что исходя из полученной параметрической зависимости 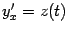 ,
, 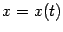 , мы можем отыскать вторую производную функции
, мы можем отыскать вторую производную функции 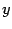 по переменной
по переменной 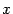 :
:
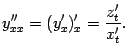
Пример 4.23 Пусть дана та же зависимость между  и
и  , что в предыдущем примере:
, что в предыдущем примере:
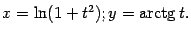
Найдём выражение для второй производной 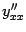 через параметр
через параметр 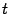 . Ранее мы получили, что
. Ранее мы получили, что 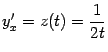 . Поэтому
. Поэтому 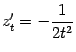 ; производную
; производную 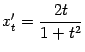 мы нашли выше. Получаем:
мы нашли выше. Получаем:
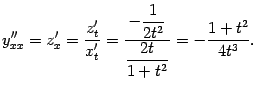
Можно получить и явный вид производной второго порядка от параметрически заданной функции, если подставить 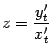 в формулу
в формулу 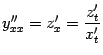 ; при этом получим:
; при этом получим:
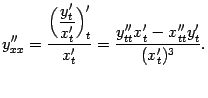
|
 2015-08-13
2015-08-13 369
369







