Содержание задания: Найти локальные экстремумы функции одной переменной. Если функция имеет бесконечное количество экстремальных точек, локализовать и найти 3 из них [1].
Теорема (необходимое условие экстремума первого порядка). Пусть функция 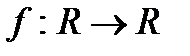 в точке
в точке 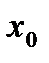 имеет локальный экстремум. Если в этой точке существует производная
имеет локальный экстремум. Если в этой точке существует производная 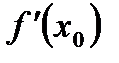 , то
, то 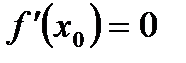 .
.
Если в точке 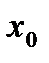 производная функции
производная функции 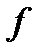 равна нулю, точку называют критической или стационарной.
равна нулю, точку называют критической или стационарной.
Для дважды дифференцируемых функций можно применить теорему о необходимых и достаточных условиях экстремума второго порядка.
Теорема (условия экстремума второго порядка). Пусть функция 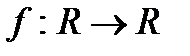 является дифференцируемой в окрестности точки
является дифференцируемой в окрестности точки 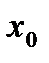 и пусть существует
и пусть существует 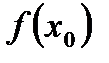 .
.
1. Если в точке 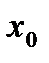 функция имеет локальный минимум, то
функция имеет локальный минимум, то 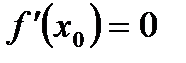 и
и 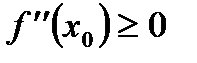 . Если в точке
. Если в точке 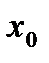 она имеет локальный максимум, то
она имеет локальный максимум, то 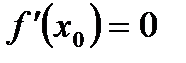 и
и 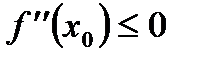 .
.
2. Если 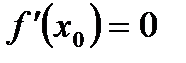 и
и 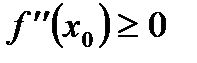 , то в точке
, то в точке 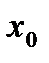 функция имеет локальный минимум. Если
функция имеет локальный минимум. Если 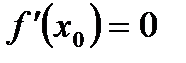 и
и 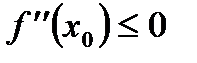 , то в точке
, то в точке 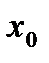 она имеет локальный максимум.
она имеет локальный максимум.
 2015-08-13
2015-08-13 539
539







