Задание 2. Нахождение локального экстремума функции двух переменных в Maple

Содержание задания: Найти локальные экстремумы функции двух переменных. Если функция имеет бесконечное количество экстремальных точек, локализовать и найти 3 из них [1],[2].

Теорема (необходимое условие экстремума первого порядка). Пусть функция 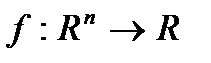в точке 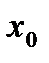имеет локальный экстремум. Если в этой точке существуют частные производная 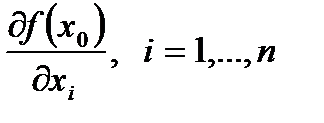, то все эти производные равны нулю.

Если в точке 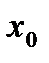все частные производные функции 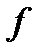равны нулю, точку называют критической или стационарной.

Теорема (условия экстремума второго порядка). Пусть функция 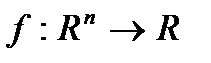определена, непрерывна и имеет непрерывные частные производные первого и второго порядка в некоторой окрестности точки .

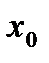1. Если в точке 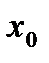функция имеет локальный минимум, то

(*)

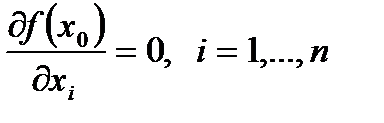и матрица частных производных второго порядка

(**)

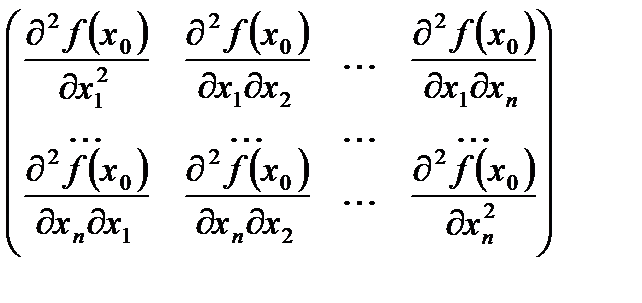неотрицательно определена.

Если в точке 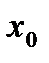она имеет локальный максимум, то выполнены условия (*) и матрица (**) неположительно определена.

2. Если выполнены условия (*) и матрица (**) положительно определена, то в точке 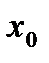функция 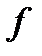имеет локальный минимум. Если выполнены условия (*) и матрица (**) отрицательно определена, то в точке 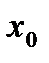функция 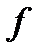имеет локальный максимум.