В магнитном поле на движущийся электрон действует сила Лоренца, равная по величине:
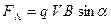 ,
,
где 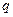 – заряд электрона;
– заряд электрона;
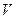 – скорость электрона;
– скорость электрона;
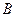 – магнитная индукция поля;
– магнитная индукция поля;
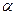 – угол между векторами
– угол между векторами 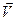 и
и 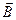 .
.
Сила Лоренца действует перпендикулярно траектории электрона, то есть является нормальной силой. Следовательно, двигаться электрон будет по винтовой линии – то есть движение электрона можно представить в виде суммы двух движений:
- равномерного движения по окружности под действием силы Лоренца в плоскости, перпендикулярной линиям поля со скоростью:
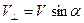 ;
;
- прямолинейного равномерного в направлении линий поля со скоростью:
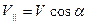 .
.
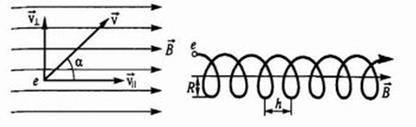
В данном случае, согласно правилу левой руки, сила Лоренца будет направлена по направлению к наблюдателю.
Движение по окружности.
Для движения по окружности по II-му закону Ньютона:
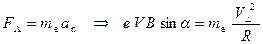 ,
,
где 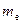 – масса электрона;
– масса электрона;
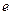 – заряд электрона;
– заряд электрона;
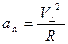 – ускорение электрона (нормальное);
– ускорение электрона (нормальное);
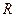 – радиус окружности.
– радиус окружности.
Отсюда выразим радиус окружности:
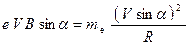 ;
;
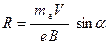 .
.
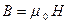 ,
,
где 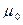 – магнитная постоянная;
– магнитная постоянная;
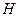 – напряжённость поля.
– напряжённость поля.
Рассчитаем радиус винтовой линии:
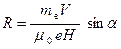 ;
;
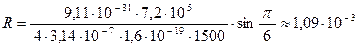 м
м 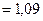 мм.
мм.
Если электрон движется по окружности радиуса 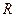 со скоростью
со скоростью 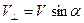 , то период вращения будет равен:
, то период вращения будет равен:
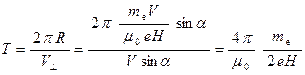 .
.
За время 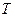 электрон в направлении линий поля пройдёт расстояние (шаг винтовой линии):
электрон в направлении линий поля пройдёт расстояние (шаг винтовой линии):
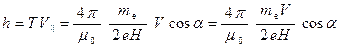 ;
;
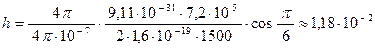 м
м 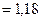 см.
см.
Ответ: 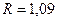 мм,
мм, 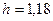 см.
см.
421. Электрон движется по окружности радиуса 1 см в однородном магнитном поле с индукцией 0,1 Тл. Параллельно магнитному полю было возбуждено электрическое поле напряжённостью 1 В/см. Определить промежуток времени, в течение которого должно действовать электрическое поле для того, чтобы кинетическая энергия электрона возросла вдвое.
| Дано: | |
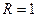 см см | 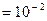 м м |
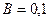 Тл Тл | |
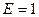 В/см В/см | 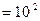 В/м В/м |
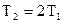 | |
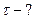 |
 2015-08-21
2015-08-21 1433
1433








