Для решения (1) и (2) строят ф-цию: 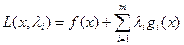 , где
, где 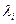 -множетель Логранджа, которые будут
-множетель Логранджа, которые будут 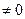 при
при 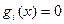 . Тогда минимизация эквивалентна миним. (1) при условии (2). Необходимое условие минимума
. Тогда минимизация эквивалентна миним. (1) при условии (2). Необходимое условие минимума 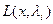 .
. 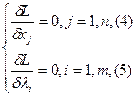
Решая эту систему получаем точки стационарности ф-и Логранджа.
Теорема. Пусть f(x) и g(x) – диферен. в 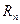 . Тогда если точка x* является решением этой задачи и Якобиан не равен 0, то сушествует вектор
. Тогда если точка x* является решением этой задачи и Якобиан не равен 0, то сушествует вектор 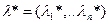 , такой что
, такой что 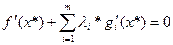 причем
причем 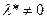
 2015-08-21
2015-08-21 438
438








