Исходными данными для работы являются:
- звено AD (стойка) имеет длину d=1;
- углы a и b, определяющие взаимное расположение звеньев AB и CD относительно стойки;
- допустимое значение угла давления шатуна на коромысло uд;
- значение коэффициента К (0 £ К £ p/2);
- значение угла j0;
- пределы изменения угла j (0 £ j £ 2p).
Результатами расчетов являются:
- длины звеньев механизма - a, b, c,
- угол давления шатуна на звено CD - u(j),
- погрешность расчетов - dq(j).
В качестве численного метода выбирается матричный метод решения систем линейных уравнений. В ходе решения задачи используется операция вычисления определенного интеграла.
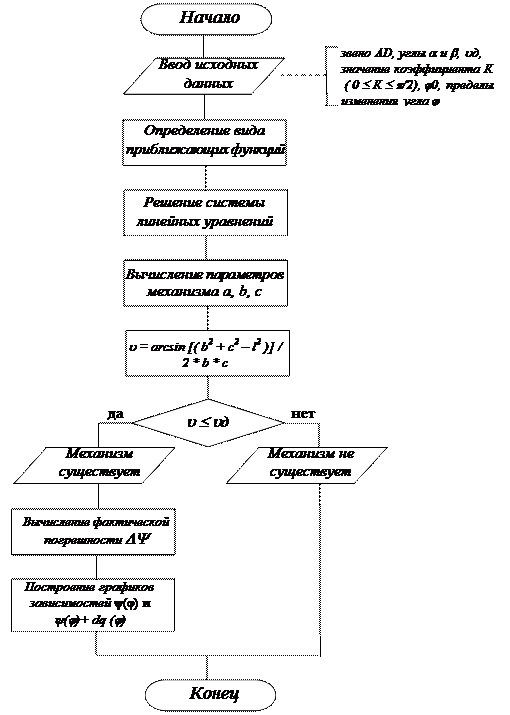
Последовательность шагов алгоритма решения задачи имеет следующий вид.
1. Задать исходные данные.
2. Задать вид приближающих функций.
3. Решить систему линейных уравнений (2.2).
4. Вычислить параметры механизма a, b, c по формуле (2.1).
5. Рассчитать по формуле (2.6) максимальное значение угла давления и проверить выполнение условия (2.7).
6. Определить фактическую погрешность по формуле (2.8).
7. Построить графики зависимостей y(j) и y(j)+ dq (j).
Данный алгоритм может быть представлен в виде графической схемы, приведенной на рисунке 3.
Реализация данного алгоритма в виде документа системы MathCAD приведена на рисунке 4.
|
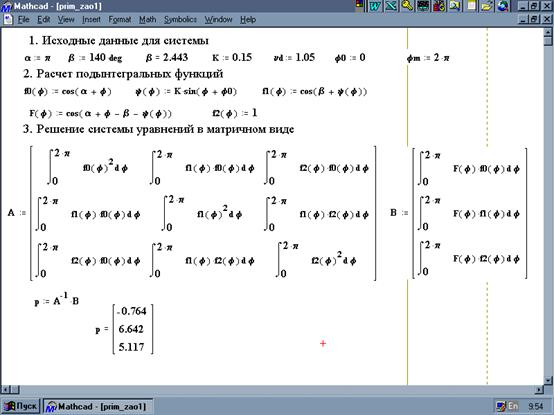
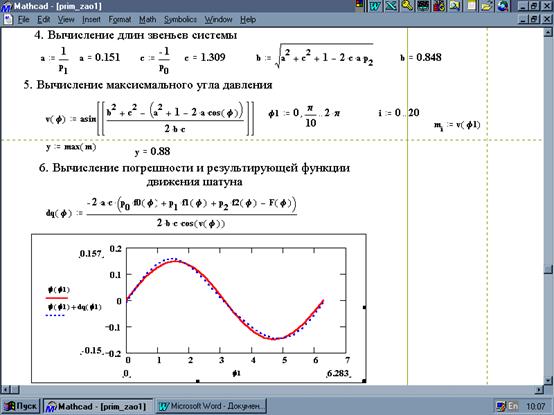
Рисунок 4 - Расчет математической модели шарнирного четырехзвенника
3.3.2 Расчет параметров линейной электрической цепи
Второй пример, наглядно демонстрирующий последовательность разработки практической части курсовой работы – решение задачи расчета параметров линейной электрической цепи. Как и в предыдущем примере, ниже приведено условие задачи, которое студент должен поместить при составлении пояснительной записки в подраздел «Полная постановка задачи» раздела «Алгоритмический анализ задачи».
2.1 Полная постановка задачи
Для заданной линейной электрической цепи (рисунок 2.1) рассчитать значения токов во всех ветвях, проверить правильность расчета по балансу электрических мощностей [5]. Математическая модель расчета цепи строится на основании закона Ома и первого закона Кирхгофа и имеет вид:
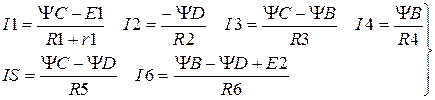 (2.1)
(2.1)
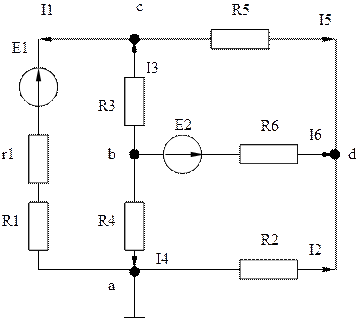 |
Система уравнений строится на основе первого закона Кирхгофа, который гласит: алгебраическая сумма токов, сходящихся в любом узле электрической цепи, равна нулю.
Рисунок 2.1 - Линейная электрическая цепь системы
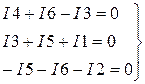 (2.2)
(2.2)
Правильность расчета токов в электрической цепи проверяется по балансу мощностей. В соответствии с законом сохранения энергии в любой электрической цепи сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей, расходуемых в приемниках энергии. Для данного примера это:
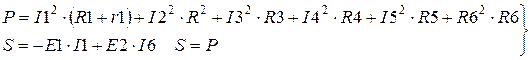 (2.3)
(2.3)
По предложенной постановке задачи студент выполняет алгоритмический анализ и создает обобщенный алгоритм с выбором численных методов для решения задачи. Алгоритм может быть приведен ив описательном виде и в виде графической схемы.
Алгоритмический анализ задачи
1) В качестве исходных данных выбираются значения сопротивлений, и мощности двух источников ЭДС.
2) Результирующими данными являются значения токов в цепи.
3) Описываются функции токов цепи с формальными параметрами напряжений в различных точках цепи.
4) Применяется блочный метод для решения системы уравнений, приведенной в постановке задачи. Результатами решения системы являются значения напряжений в цепи.
5) Вычисляются конкретные числовые значения токов в цепи по описанным функциональным зависимостям.
Графическая схема алгоритма решения задачи приведена на рисунке Реализация данного алгоритма в виде документа системы MathCAD приведена на рисунке 5.
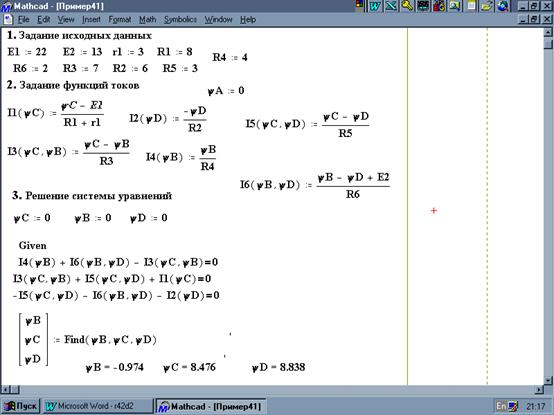 |
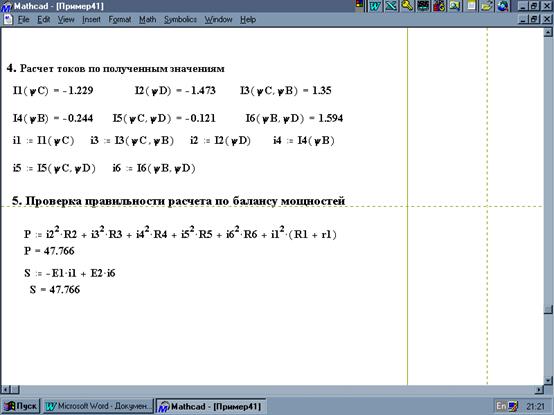
Рисунок 5 - Расчет параметров линейной цепи в MathCAD
 2015-08-21
2015-08-21 1534
1534
