Критерий Найквиста

Это частотный критерий суждения об устойчивости и о многом другом происходит по частотным характеристикам: по годографу Найквиста. Он занимался задачей проектирования усилителя.

По критерию Найквиста суждения об устойчивости замкнутой системы происходит по годографу разомкнутой:

1) Судят об устойчивости замкнутой с-п.

2) Что сделать за счёт замкнутой, чтоб она была устойчива.

Пусть передаточная функция разомкнутой системы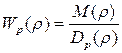

Передаточная функция замкнутой цепи при единичной обратной связи.

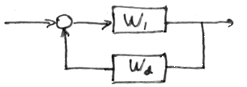
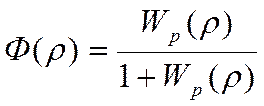
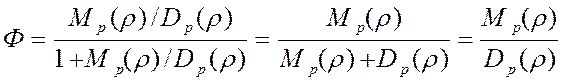
Рассмотрим частотную хар-ку:

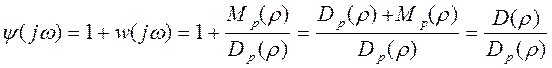-- отношение хар-го полинома замкнутой системы к хар-му полиному разомкнутой системы.

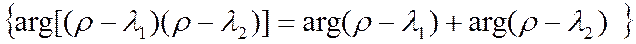
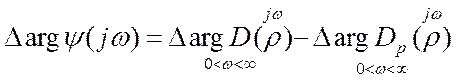(2)

Приращение аргумента хар-го полинома разомкнутой системы равна …. (см. выше).

Если разомкнутая система устойчива, то приращение аргумента равно:

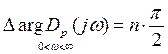, где n -порядок характерного уравнения.

Порядок хар-ого уравнения замкнутой и разомкнутой системы совпадает.

Для того, чтоб замкнутая система была устойчивой, все корни хар-ого уравнения должны лежать в левой полуплоскости, т.е.

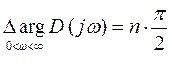
Для того, чтобы система устойчивая в разомкнутом состоянии была устойчива в разомкнутом состоянии, необходимо и достаточно, чтобы:

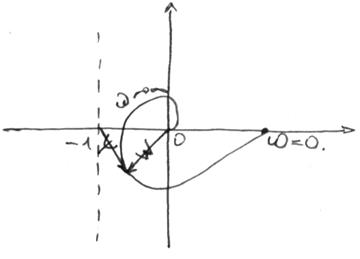
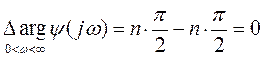
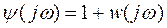
Годограф 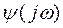и годограф 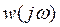совпадают если сместить ось ординат на единицу влево. При изменении 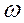от 0 до 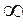годограф 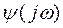описывает кривую и ее приращение (угол поворота) должен равняться 0 (с нуля начался в ноль пришел)

Вектор 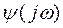не должен охватывать (.)

(-1; jo)

(*)

Необходимо и достаточно, чтобы вектор 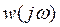не охватывал точку (-1; jo).

Пусть разомкнутая система не устойчива и имеет n корней в правой полуплоскости, тогда приращением аргумента хар-го полинома разомкнутой системы равно:

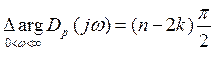
Если замкнутая система устойчива, то приращение аргумента замкнутой системы равно:

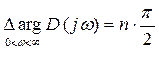
В соответствии с уравнением (2), для того, чтобы система не устойчивая в разомкнутом состоянии и имеющая n корней в правой полуплоскости, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы:

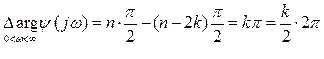
или (что тоже самое) годограф 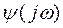должен охватить начало координат k/2 раз.

Для того чтобы система устойчивая в разомкнутом состоянии, с k корнями в правой полуплоскости, была устойчива в разомкнутом состоянии необходимо и достаточно, чтобы частотная хар-ка 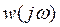охватила точку (-1; jo) k/2 раз в положительном направлении; k – число корней хар-го уравнения в правой полуплоскости.

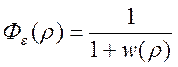-- передаточная функция по ошибке.

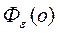-- коэффициент статической ошибки

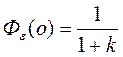
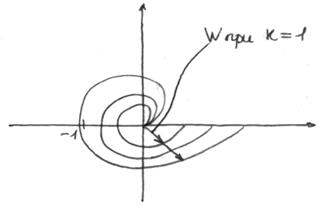
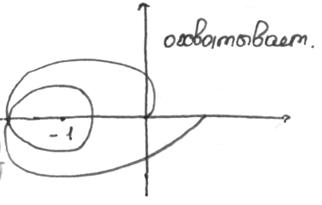
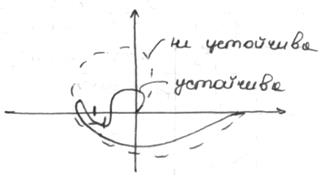Системы в которых увеличение коэффициента усиления не приводит к захвату -1, называются абсолютно устойчивыми (системы 2-й степени).

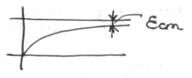
Путем введения звеньев можно перейти к устойчивой системе (рис. см. выше). В статических системах при 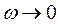хар-ка стремится к номинальному числу.

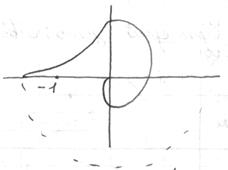В астатических начинается от стр. в 0.

.

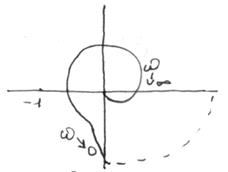
Не охватывает, астатизм первого порядка Охватывает, астатизм 2-го порядка.