Определение 8.3. Совокупность линейно независимых векторов, порожда-ющих линейное пространство V, называют базисом этого пространства. Если u 1, u 2,..., u n – базис пространства V, то любой вектор х из V может быть представлен в виде линейной комбинации векторов u 1, u 2,..., u n:
x = 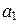 u 1 +
u 1 + 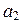 u 2 +... +
u 2 +... + 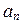 u n =
u n = 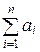 u i. (8.5)
u i. (8.5)
В разложении (8.5) числа 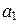 ,
, 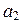 ,...,
,..., 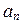 называются координатами, или компонентами, вектора х в базисе u 1, u 2,..., u n.
называются координатами, или компонентами, вектора х в базисе u 1, u 2,..., u n.
Докажем единственность представления (8.5). Допустим, что х можно представить еще и в виде х = b 1 u 1 + b 2 u 2 +... + bn u n. Вычтем это равенство из соотношения (8.5) и получим (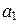 – b 1) u 1 + (
– b 1) u 1 + (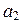 – b 2) u 2 +... + (
– b 2) u 2 +... + (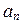 – bn) u n = 0. Так как векторы u 1, u 2,..., u n линейно независимы, то
– bn) u n = 0. Так как векторы u 1, u 2,..., u n линейно независимы, то 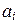 = bi, i = 1, 2,..., п.
= bi, i = 1, 2,..., п.
Как и в R 3, линейные операции над векторами пространства V при заданном базисе приводят к обычным линейным операциям над числами – координатами этих векторов в данном базисе, т. е. если
x = 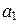 u 1 +
u 1 + 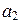 u 2 +... +
u 2 +... + 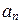 u n, у = b 1 u 1 + b 2 u 2 +...+ bn u n,
u n, у = b 1 u 1 + b 2 u 2 +...+ bn u n,
то
х + у = (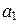 + b 1) u 1 + (
+ b 1) u 1 + (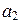 + b 2) u 2 +… + (
+ b 2) u 2 +… + (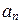 + bn) u n,
+ bn) u n,
 x = (
x = (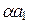 ) u 1 + (
) u 1 + (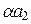 ) u 2+... + (
) u 2+... + (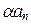 ) u n. (8.6)
) u n. (8.6)
Учитывая взаимно однозначное соответствие между вектором и его координатами в выбранном базисе u 1, u 2,..., u n, будем писать
x = 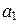 u 1 +
u 1 + 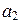 u 2 +... +
u 2 +... + 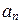 u n
u n 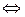 х = (
х = (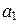 ,
, 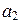 ,...,
,..., 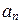 ). (8.7)
). (8.7)
Теорема 8.2. Если линейное пространство V имеет базис, состоящий из n элементов, то всякие р векторов из V при р > n линейно зависимы.
Доказательство. Согласно утверждению 2 теоремы 8.1, можно считать, что р = n + 1. Рассмотрим случай, когда пространство V имеет базис, состоящий из единственного элемента u. Тогда для любых x 1 и x 2 имеем x 1 = 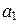 u и x 2 =
u и x 2 = 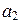 u. Если
u. Если 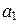 и
и 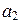 не равны нулю, то
не равны нулю, то 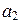 x 1 –
x 1 – 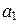 x 2 = 0 и, значит, векторы x 1 и x 2 линейно зависимы. Если же
x 2 = 0 и, значит, векторы x 1 и x 2 линейно зависимы. Если же 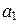 = 0 или
= 0 или 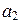 = 0, то векторы x 1 и x 2 тоже линейно зависимы, т. к. среди них есть нулевой вектор (утверждение 1 теоремы 8.1).
= 0, то векторы x 1 и x 2 тоже линейно зависимы, т. к. среди них есть нулевой вектор (утверждение 1 теоремы 8.1).
Дальнейшие рассуждения продолжаем по индукции. Допустим, что в пространстве, базис которого состоит из n – 1 элементов, n векторов линейно зависимы. Рассмотрим пространство V, имеющее базис u 1, u 2,..., u n. Пусть n + 1 элементов из V имеют вид
х т = am 1 u 1 + am 2 u 2 +... + amn u n, т = 1, 2,..., n + 1.
Если в этом равенстве все коэффициенты amn, т = 1, 2,..., n, n + 1, равны нулю, то векторы x 1, x 2,…, x n, x n +1 принадлежат пространству, порожденному элементами u 1, u 2,..., u n –1. Следовательно, по предположению индукции они линейно зависимы. Пусть теперь хотя бы один из коэффициентов amn, например a ( n +1) n, отличен от нуля. Рассмотрим векторы
у m = х т 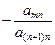 x n +1, m = 1, 2, …, n.
x n +1, m = 1, 2, …, n.
Коэффициенты при n -м элементе u n базиса в разложениях векторов у m равны нулю, и, значит, по предположению индукции векторы y 1, y 2,..., y n линейно зависимы. В таком случае существуют n чисел  ,
,  ,…
,… 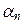 , не все равные нулю, которые удовлетворяют равенству
, не все равные нулю, которые удовлетворяют равенству  y 1 +
y 1 +  y 2 +... +
y 2 +... + 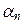 y n = 0. Отсюда следует, что
y n = 0. Отсюда следует, что
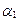 x 1 +
x 1 + 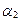 x 2 +… +
x 2 +… + 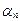 x n
x n 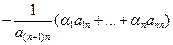 x n +1 = 0.
x n +1 = 0.
А т. к. не все числа  ,
,  ,…,
,…, 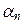 равны нулю, то векторы x 1, x 2,…, x n, x n +1 являются линейно зависимыми.¨
равны нулю, то векторы x 1, x 2,…, x n, x n +1 являются линейно зависимыми.¨
Следствие 1. Если пространство V имеет базис из n элементов и если р векторов из V линейно независимы, то 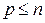 .
.
Следствие 2. Если линейное пространство V имеет некоторый базис из n элементов, то и всякий другой базис пространства V состоит из n элементов.
Доказательство. Если v 1, v 2,…, v p – другой базис пространства V, то векторы v 1, v 2,…, v p линейно независимы и по предыдущему следствию 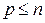 . Поменяв местами базисы v 1, v 2,…, v p и u 1, u 2,..., u n, получаем, что
. Поменяв местами базисы v 1, v 2,…, v p и u 1, u 2,..., u n, получаем, что 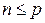 . Значит, р = n. ¨
. Значит, р = n. ¨
Определение 8.4. Если V – линейное пространство с конечным базисом, то число n элементов этого базиса называется размерностью пространства V. Размерность обозначается dim V (от англ. dimension – «размерность»).
Линейное пространство V называется бесконечномерным, если в нем существует любое число линейно независимых векторов.
Теорема 8.3. Любую систему из k линейно независимых векторов u 1, u 2,..., u k, k < n, n -мерного пространства V можно дополнить до базиса этого пространства.
Доказательство. Пусть k < n. Допустим, что к векторам u 1, u 2,..., u k нельзя добавить вектор u k +1, такой, что векторы u 1, u 2,..., u k, u k +1 будут линейно зависимы. Это значит, что в пространстве V имеется только k линейно независимых векторов, т. е. dim V = k < n, что противоречит условию теоремы. Следовательно, к векторам u 1, u 2,..., u k можно добавить вектор u k +1Î V, такой, что система векторов u 1, u 2,..., u k, u k +1 линейно независима. Если k + 1 < n, то, повторяя предыдущие рассуждения, получим, что можно добавить еще один вектор u k +2 Î V так, что векторы u 1, u 2,..., u k, u k +1, u k +2 линейно независимы. После конечного числа шагов получим ровно n линейно независимых векторов u 1, u 2,…, u k, u k +1,…, u n, образующих, по определению, базис пространства V. ¨
Приведем примеры базисов конкретных линейных пространств.
Пример 5. В пространстве R 3 базис образует тройка единичных взаимно ортогональных векторов i, j, k. Любой вектор x Î R 3 имеет вид x = a i + b j + g k, где a, b, g – проекции вектора на оси координат.·
Пример 6. В пространстве R n базисом служит система векторов (8.4), т. к. эти векторы, как показано выше, линейно независимы, и для любого x Î R n справедливо разложение (8.5): x = (x 1, x 2,…, xn) = x 1 е l + x 2 е 2 +... + xn е n. ·
Пример 7. Пусть Pn (x) – пространство многочленов степени не выше n. В примере 3 показано, что векторы 1, x, x 2,..., xn линейно независимы. Каждый многочлен f (x)Î Pn (x) линейно выражается через них очевидным образом: f (x) = а 0 + + 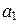 x +
x + 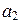 x 2 +… +
x 2 +… + 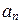 xn, где аi, i = 0, 1,…, n, – коэффициенты f (x). Отсюда следует, что векторы 1, x, x 2,..., xn образуют базис пространства Pn (x) и dim Pn (x) = n + 1.·
xn, где аi, i = 0, 1,…, n, – коэффициенты f (x). Отсюда следует, что векторы 1, x, x 2,..., xn образуют базис пространства Pn (x) и dim Pn (x) = n + 1.·
Пример 8. Примером бесконечномерного пространства может служить пространство C [ a ; b ]. В самом деле, для любого натурального числа n система 1, x, x 2,..., xn, состоящая из n + 1 векторов этого пространства, как показано в примере 3, является линейно независимой.·
 2015-08-21
2015-08-21 4035
4035
