Определение 8.5. Подnространством линейного nространства V называется всякое непустое подмножество 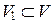 , обладающее следующими свойствами:
, обладающее следующими свойствами:
1°. Если x, y  V 1, то x + y
V 1, то x + y  V 1.
V 1.
2°. Если x  V 1,
V 1, 
 R, то
R, то  x
x  V 1.
V 1.
Убедимся, что подпространство 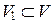 , удовлетворяющее требованиям 1° и 2°, само является линейным пространством. Действительно, аксиомы 1°, 2°, 5°–8° линейного пространства для векторов из V 1, очевидно, выполняются. Надо убедиться только в том, что нулевой вектор принадлежит V 1 и что для любого x
, удовлетворяющее требованиям 1° и 2°, само является линейным пространством. Действительно, аксиомы 1°, 2°, 5°–8° линейного пространства для векторов из V 1, очевидно, выполняются. Надо убедиться только в том, что нулевой вектор принадлежит V 1 и что для любого x  V 1 существует противоположный элемент (– x)
V 1 существует противоположный элемент (– x)  V 1.
V 1.
В самом деле, если x  V 1, то произведения
V 1, то произведения 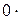 x = 0 и (– 1) x = – x также принадлежат V 1.
x = 0 и (– 1) x = – x также принадлежат V 1.
Приведем примеры подпространств линейных пространств.
Пример 9. Пусть V = R 2. В этом пространстве рассмотрим множества V 1 и V 2 всех векторов вида a = (x, 0) и вида b = (0, y) соответственно. Любые векторы a 1 = (x 1, 0), a 2 = (x 2, 0) и a = (x, 0) из V 1 обладают свойствами
a 1 + a 2 = (x 1 + x 2, 0)  V 1;
V 1;  a = (
a = ( x, 0)
x, 0)  V 1,
V 1, 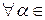 R.
R.
Аналогично, для всех векторов b 1 = (0, y 1), b 2 = (0, y 2) и b = (0, y) из V 2 имеем
b 1 + b 2 = (0, y 1 + y 2)  V 2;
V 2;  b = (0,
b = (0,  у)
у)  V 2,
V 2, 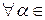 R.
R.
Таким образом, V 1 и V 2 – подпространства пространства R 2. Подпространство V 1 состоит из всех векторов, параллельных оси Ox, а подпространство V 2 образуют все векторы, параллельные оси Oy. ·
Пример 10. Пусть V = R 3. Векторы вида a = (x, 0, 0), вида b = (0, у, 0) и вида с = (0, 0, z) образуют три самостоятельных линейных подпространства в R 3, состоящих из всех векторов, параллельных осям Ox, Oy и Oz соответственно. Аналогично, векторы вида a 1 = (0, у, z), вида b 1 = (x, 0, z) и вида c 1 = (x, y, 0) образуют линейные подпространства в R 3, состоящие из всех векторов, параллельных плоскостям Oyz, Oxz и Oxy соответственно. ·
Пример 11. Пусть V = C[a; b], а V 1 – подмножество функций f из C [ a ; b ], таких, что f (x 0) = 0 для фиксированного x 0  [ а; b ]. Если f 1(x 0) = 0, f 2(x 0) = 0, то f 1(x 0) + f 2(x 0) = = 0 и
[ а; b ]. Если f 1(x 0) = 0, f 2(x 0) = 0, то f 1(x 0) + f 2(x 0) = = 0 и  f 1(x 0) = 0,
f 1(x 0) = 0, 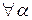
 R. Значит, V 1 – подпространство пространства C [ a ; b ]. ·
R. Значит, V 1 – подпространство пространства C [ a ; b ]. ·
Если в n -мерном пространстве V всякие n + 1 векторов линейно зависимы, то это утверждение и подавно выполнено в подпространстве 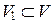 , т. е. dim V 1
, т. е. dim V 1 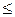 dim V. Другими словами, размерность подпространства не превосходит размерности самого линейного пространства.
dim V. Другими словами, размерность подпространства не превосходит размерности самого линейного пространства.
Важным в теории линейных пространств является понятие линейной оболочки.
Определение 8.6. Пусть x 1, x 2,…, x k – система векторов линейного пространства V. Линейной оболочкой, порожденной векторами x 1, x 2,…, x k, называется совокупность всех линейных комбинаций вида y =  x 1 +
x 1 +  x 2 +… +
x 2 +… + 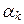 x k, где
x k, где  ,
,  ,...,
,..., 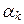 – любые числа из R, и обозначается L (x 1, x 2,…, x k).
– любые числа из R, и обозначается L (x 1, x 2,…, x k).
Легко показать, что линейная оболочка L (x 1, x 2,…, x k) является подпро-странством линейного пространства V.
Пусть y l = 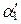 x 1 +
x 1 + 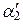 x 2 +… +
x 2 +… + 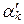 x k, y 2 =
x k, y 2 = 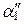 x 1 +
x 1 + 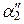 x 2 +… +
x 2 +… + 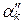 x k – произвольные элементы из L (x 1, x 2,…, x k). Тогда по аксиомам 5°, 7°, 8° линейного пространства
x k – произвольные элементы из L (x 1, x 2,…, x k). Тогда по аксиомам 5°, 7°, 8° линейного пространства
y l + y 2 = 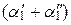 x 1 +
x 1 + 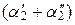 x 2 +…+
x 2 +…+ 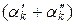 x k
x k  L (x 1, x 2,…, x k);
L (x 1, x 2,…, x k);
 y l =
y l = 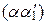 x 1 +
x 1 + 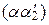 x 2 +…+
x 2 +…+ 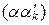 x k
x k  L (x 1, x 2,…, x k),
L (x 1, x 2,…, x k), 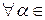 R.
R.
Следовательно, L (x 1, x 2,…, x k) – подпространство линейного пространства V, а, значит, dim L 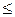 dim V, причем dim L = k тогда и только тогда, когда векторы x 1, x 2,…, x k линейно независимы.
dim V, причем dim L = k тогда и только тогда, когда векторы x 1, x 2,…, x k линейно независимы.
 2015-08-21
2015-08-21 2381
2381
