Определение 8.2. Пусть x 1, x 2,…, x n – векторы линейного пространства V и  ,
,  ,…,
,…, 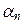 – произвольные действительные числа. Вектор
– произвольные действительные числа. Вектор
y =  x 1 +
x 1 +  x 2 +… +
x 2 +… + 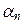 x n =
x n = 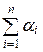 x i (8.1)
x i (8.1)
называется линейной комбинацией векторов x 1, x 2,…, x n, а числа  ,
,  ,…,
,…, 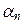 – коэффициентами линейной комбинации. Говорят, что множество векторов x 1, x 2,…, x n порождает пространство V, если каждый вектор y из V может быть представлен в виде (8.1). Векторы x 1, x 2,…, x n линейного пространства V называются линейно зависимыми, если существуют числа
– коэффициентами линейной комбинации. Говорят, что множество векторов x 1, x 2,…, x n порождает пространство V, если каждый вектор y из V может быть представлен в виде (8.1). Векторы x 1, x 2,…, x n линейного пространства V называются линейно зависимыми, если существуют числа  ,
,  ,…,
,…, 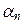 , не все равные нулю, такие, что
, не все равные нулю, такие, что
 x 1 +
x 1 +  x 2 +… +
x 2 +… + 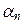 x n = 0. (8.2)
x n = 0. (8.2)
Если же равенство (8.2) выполняется лишь в единственном случае, когда  =
=  =... =
=... = 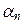 = 0, то векторы x 1, x 2,…, x n называются линейно независимыми.
= 0, то векторы x 1, x 2,…, x n называются линейно независимыми.
Понятие линейной зависимости векторов в R 3 введено в §2.2. Там же показано, что если векторы линейно зависимы, то один из них является линейной комбинацией остальных векторов.
Это доказательство дословно переносится на случай любого линейного пространства V.
Верно и обратное: если один из векторов x 1, x 2,…, x n является линейной комбинацией остальных, то указанные векторы линейно зависимы.
Действительно, пусть, например, x 1 =  x 2 +
x 2 + 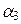 x 3 +… +
x 3 +… + 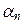 x n. Тогда (– 1) x 1 + +
x n. Тогда (– 1) x 1 + +  x 2 +… +
x 2 +… + 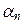 x n = 0. Так как – 1 ¹ 0, то последнее равенство и устанавливает линейную зависимость векторов x 1, x 2,…, x n.
x n = 0. Так как – 1 ¹ 0, то последнее равенство и устанавливает линейную зависимость векторов x 1, x 2,…, x n.
Теорема 8.1. Справедливы следующие утверждения:
1. Если среди векторов x 1, x 2,…, x n содержится нулевой вектор, то они линейно зависимы.
2. Если среди векторов x 1, x 2,…, x n имеется k (k < п) линейно зависимых векторов, то и вся система векторов x 1, x 2,…, x n линейно зависима.
3. Если векторы x 1, x 2,…, x n линейно независимы, то и любая часть этой системы векторов линейно независима.
Доказательство.
1. Если вектор x k = 0, то из равенства 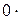 x 1 +... +
x 1 +... + 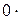 x k –1 +
x k –1 + 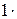 x k +… +
x k +… + 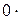 x n = 0 вытекает линейная зависимость векторов x 1, x 2,…, x n.
x n = 0 вытекает линейная зависимость векторов x 1, x 2,…, x n.
2. Пусть векторы x 1, x 2,…, x k, k < п, линейно зависимы. Тогда из равенства  x 1 +
x 1 +  x 2 +… +
x 2 +… + 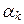 x k = 0, в котором среди чисел
x k = 0, в котором среди чисел  ,
,  ,...,
,..., 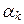 хотя бы одно не равно нулю, получим равенство
хотя бы одно не равно нулю, получим равенство  x 1 +
x 1 +  x 2 +… +
x 2 +… + 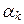 x k +
x k + 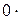 x k +1 +... +
x k +1 +... + 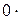 x n = 0, которое и означает линейную зависимость всей системы векторов x 1, x 2,…, x n.
x n = 0, которое и означает линейную зависимость всей системы векторов x 1, x 2,…, x n.
3. Пусть векторы x 1, x 2,…, x n линейно независимы. Если бы некоторая часть этих векторов была линейно зависимой, то на основании утверждения 2 вся система x 1, x 2,…, x n была бы линейно зависимой, что не так.¨
Рассмотрим некоторые примеры, поясняющие понятие линейной зависимости векторов.
Пример 1. В линейном пространстве R 3 векторы x 1 = (1, – 1, 0), x 2 = (2, 1, 3) и x 3 = (14, – 2, 12), очевидно, линейно зависимы, т. к. имеет место равенство
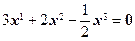 .·
.·
Пример 2. Три функции f 1(x) = 1, f 2(x) = cos2 х, f 3(x) = sin2 х в пространстве C [ a ; b ], где [ a; b ] – произвольный отрезок, линейно зависимы, поскольку
f 1(x) – f 2(x) – 2 f 3(x) = 0, " x Î R. ·
Пример 3. Покажем, что в пространстве C [ a ; b ] векторы у 1 = 1, у 2 = х, у 3 = = x 2,..., у n +1 = xn, где n – любое натуральное число, [ a; b ] – произвольный отрезок, линейно независимы. Для этого достаточно убедиться в том, что равенство
 × 1 +
× 1 +  x +
x + 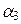 x 2 +…+
x 2 +…+ 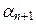 xn = 0, " x Î R, (8.3)
xn = 0, " x Î R, (8.3)
возможно лишь при  =
=  =... =
=... = 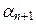 = 0.
= 0.
Действительно, полагая в равенстве (8.3) х 0 = 0, получаем  = 0. Тогда находим (
= 0. Тогда находим ( +
+ 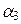 x +... +
x +... + 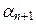 xn –1) x = 0,
xn –1) x = 0, 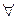 x Î R. Последнее соотношение для всех х Î R возможно, если
x Î R. Последнее соотношение для всех х Î R возможно, если  +
+ 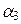 x +... +
x +... + 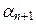 xn –1 = 0. Полагая здесь снова х 0 = 0, получаем
xn –1 = 0. Полагая здесь снова х 0 = 0, получаем  = 0. Продолжая эти рассуждения, на (n + 1)-м шаге имеем
= 0. Продолжая эти рассуждения, на (n + 1)-м шаге имеем 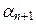 = 0, т. е. равенство (8.3) возможно только при
= 0, т. е. равенство (8.3) возможно только при  =
=  =... =
=... = 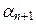 = 0.·
= 0.·
Пример 4. В пространстве R n рассмотрим векторы
е l = (1, 0,..., 0), е 2 = (0, 1,..., 0),..., е n = (0, 0,..., 1). (8.4)
Покажем, что они линейно независимы. Действительно, пусть  ,
,  ,...,
,..., 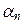 – произвольные действительные числа. Тогда
– произвольные действительные числа. Тогда
 е l +
е l +  е 2 +...+
е 2 +...+ 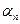 е n = 0
е n = 0 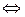
 (1, 0,..., 0) +
(1, 0,..., 0) +  (0, 1,..., 0) +...+
(0, 1,..., 0) +...+ 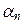 (0, 0,..., 1) =
(0, 0,..., 1) =
= (0, 0,..., 0) 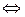 (
( ,
,  ,...,
,..., 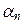 ) = (0, 0,..., 0)
) = (0, 0,..., 0) 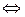
 =0 &
=0 &  =0 &... &
=0 &... & 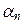 =0,
=0,
т. е. векторы е l, е 2,..., е n линейно независимы.·
 2015-08-21
2015-08-21 2729
2729
