Глава 3. Линейные векторные пространства
Тема 8. Линейные векторные пространства
Определение линейного пространства. Примеры линейных пространств
В §2.1 определены операция сложения свободных векторов из R 3 и операция умножения векторов на действительные числа, а также перечислены свойства этих операций. Распространение этих операций и их свойств на множество объектов (элементов) произвольной природы приводит к обобщению понятия линейного пространства геометрических векторов из R 3, определенного в §2.1. Сформулируем определение линейного векторного пространства.
Определение 8.1. Множество V элементов х, у, z,... называется линейным векторным пространством, если:
имеется правило, которое каждым двум элементам x и у из V ставит в соответствие третий элемент из V, называемый суммой х и у и обозначаемый х + у;
имеется правило, которое каждому элементу x 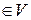 и любому действительному числу
и любому действительному числу  ставит в соответствие элемент из V, называемый произведением элемента х на число
ставит в соответствие элемент из V, называемый произведением элемента х на число  и обозначаемый
и обозначаемый  x.
x.
При этом сумма любых двух элементов х + у и произведение  x любого элемента на любое число должны удовлетворять следующим требованиям – аксиомам линейного пространства:
x любого элемента на любое число должны удовлетворять следующим требованиям – аксиомам линейного пространства:
1°. х + у = у + х (коммутативность сложения).
2°. (х + у) + z = х + (у + z) (ассоциативность сложения).
3°. Существует элемент 0 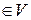 , называемый нулевым, такой, что
, называемый нулевым, такой, что
х + 0 = х, 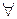 x
x 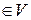 .
.
4°. Для любого x 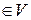 существует элемент (– х), называемый противоположным для х, такой, что
существует элемент (– х), называемый противоположным для х, такой, что
х + (– х) = 0.
5°.  (
(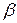 x) = (
x) = (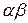 ) x,
) x, 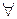 x
x 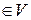 ,
, 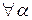 ,
, 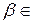 R.
R.
6°. 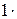 x = x,
x = x, 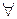 x
x 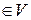 .
.
7°. (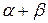 ) x =
) x =  x +
x + 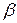 x,
x, 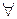 x
x 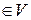 ,
, 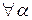 ,
, 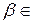 R.
R.
8°.  (х + у) =
(х + у) =  x +
x +  y,
y, 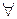 x, y
x, y 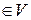 ,
, 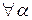
 R.
R.
Элементы линейного пространства будем называть векторами независимо от их природы.
Из аксиом 1°–8° следует, что в любом линейном пространстве V справедливы следующие свойства:
1) существует единственный нулевой вектор;
2) для каждого вектора x 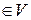 существует единственный противоположный вектор (– х)
существует единственный противоположный вектор (– х) 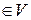 , причем (– х) = (– l) х;
, причем (– х) = (– l) х;
3) для любого вектора х справедливо равенство 0× х = 0.
Докажем, например, свойство 1). Допустим, что в пространстве V существуют два нуля: 0 1 и 0 2. Положив в аксиоме 3° х = 0 1, 0 = 0 2, получим 0 1 + 0 2 = 0 1. Аналогично, если х = 0 2, 0 = 0 1, то 0 2 + 0 1 = 0 2. Учитывая аксиому 1°, получаем 0 1 = 0 2.
Доказательство свойств 2) и 3) рекомендуется провести читателю самостоятельно.
Приведем примеры линейных пространств.
1. Множество действительных чисел образует линейное пространство R. Аксиомы 1°–8° в нем, очевидно, выполняются.
2. Множество свободных векторов трехмерного пространства, как показано в §2.1, также образует линейное пространство, обозначаемое R 3. Нулем этого пространства служит нулевой вектор.
Множество векторов на плоскости и на прямой также являются линейными пространствами. Будем обозначать их R 1 и R 2 соответственно.
3. Обобщением пространств R 1, R 2 и R 3 служит пространство R n, n  N, называемое арифметическим n-мерным пространством, элементами (векторами) которого являются упорядоченные совокупности n произвольных действительных чисел (x 1,…, xn), т. е.
N, называемое арифметическим n-мерным пространством, элементами (векторами) которого являются упорядоченные совокупности n произвольных действительных чисел (x 1,…, xn), т. е.
R n = {(x 1,…, xn) | xi  R, i = 1,…, n }.
R, i = 1,…, n }.
Удобно использовать обозначение x = (x 1,…, xn), при этом xi называется i-й координатой (компонентой) вектора x.
Для х, у  R n и
R n и 
 R определим сложение и умножение на число следующими формулами:
R определим сложение и умножение на число следующими формулами:
х + у = (x 1 + y 1,…, xn + yn);
 x = (
x = ( x 1,…,
x 1,…,  xn).
xn).
Нулевым элементом пространства R n является вектор 0 = (0,…, 0). Равенство двух векторов х = (x 1,…, xn) и у = (y 1,…, yn) из R n, по определению, означает равенство соответствующих координат, т. е. х = у Û x 1 = y 1 &… & xn = yn.
Выполнение аксиом 1°–8° здесь очевидно.
4. Пусть C [ a ; b ] – множество вещественных непрерывных на отрезке [ a; b ] функций f: [ a; b ] 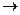 R.
R.
Суммой функций f и g из C [ a ; b ] называется функция h = f + g, определяемая равенством
h = f + g Û h (x) = (f + g)(x) = f (х) + g (x), " x Î [ a; b ].
Произведение функции f Î C [ a ; b ] на число a Î R определяется равенством
u =  f Û u (х) = (
f Û u (х) = ( f)(х) =
f)(х) =  f (x), " x Î [ a; b ].
f (x), " x Î [ a; b ].
Так введенные операции сложения двух функций и умножения функции на число превращают множество C [ a ; b ] в линейное пространство, векторами которого являются функции. Аксиомы 1°–8° в этом пространстве, очевидно, выполняются. Нулевым вектором этого пространства является тождественно нулевая функция, а равенство двух функций f и g означает, по определению, следующее:
f = g 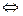 f (x) = g (x), " x Î [ a; b ].
f (x) = g (x), " x Î [ a; b ].
 2015-08-21
2015-08-21 8270
8270