Определение 8.7. Пусть V 1 и V 2 – два линейных пространства. Пересечением этих пространств называется совокупность 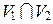 всех векторов x, принадлежащих как V 1, так и V 2, т. е.
всех векторов x, принадлежащих как V 1, так и V 2, т. е.
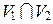 = { x | x
= { x | x  V 1 & x
V 1 & x  V 2}.
V 2}.
Совокупность всех векторов вида y + z, где y  V 1, z
V 1, z  V 2, называется суммой пространств V 1 и V 2 и обозначается V 1 + V 2, т. е.
V 2, называется суммой пространств V 1 и V 2 и обозначается V 1 + V 2, т. е.
V 1 + V 2 = { y + z | y  V 1, z
V 1, z  V 2}.
V 2}.
Покажем, что 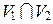 образует линейное пространство, являющееся под-пространством как V 1, так и V 2. В самом деле, если x и y принадлежат
образует линейное пространство, являющееся под-пространством как V 1, так и V 2. В самом деле, если x и y принадлежат 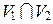 , то они принадлежат и V 1, и V 2. Поэтому вектор x + y и вектор
, то они принадлежат и V 1, и V 2. Поэтому вектор x + y и вектор  x,
x, 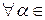 R, также принадлежат и V 1, и V 2, т. е. x + y
R, также принадлежат и V 1, и V 2, т. е. x + y 
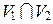 и
и  x
x 
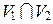 .
.
Пример 12. Пусть V 1 – пространство всех векторов вида a = (x, 0, z), V 2 – пространство всех векторов вида b = (0, y, z). Тогда суммой этих пространств является множество векторов вида a + b = (x, у, 2 z), т. е. V 1 + V 2 = R 3. Пересечение пространств V 1 и V 2 есть множество векторов вида (0, 0, z), т. е. 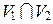 – множество всех векторов, параллельных оси Oz. ·
– множество всех векторов, параллельных оси Oz. ·
Определение 8.8. Подпространства V 1 и V 2 линейного пространства V называются дополнительными в V, если выполнены соотношения
V 1 + V 2 = V, 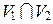 = 0, 0
= 0, 0 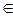 V.
V.
В этом случае говорят, что пространство V представлено в виде прямой суммы подпространств V 1 и V 2.
Пример 13. В пространстве R 3 выделим плоскость Оху (рис. 8.1). Рассмотрим в R 3 линейное подпространство R 1 векторов вида z = (0, 0, z), направленных параллельно оси Oz. Векторы на плоскости R 2 имеют вид u = (x, у, 0). Общим вектором пространств R 1 и R 2 является, очевидно, нулевой вектор 0 = = (0, 0, 0). Пусть а = (x, у, z) – любой вектор из R 3.
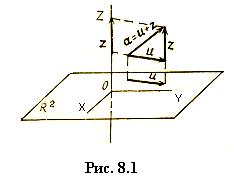 |
Тогда a = (x, у, z) = (x, у, 0) + (0, 0, z) = u + z. Таким образом, R 3 можно представить в виде прямой суммы подпространств R 1 и R 2. ·
Теоремa 8.4. Для того чтобы пространство V являлось прямой суммой подпространств V 1 и V 2, необходимо и достаточно, чтобы всякий элемент x  V единственным образом представлялся в виде
V единственным образом представлялся в виде
x = x 1 + x 2, где x 1  V 1, x 2
V 1, x 2  V 2.
V 2.
Доказательство. Необходимость. Пусть V 1 + V 2= V, 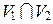 = 0. Предположим, что x
= 0. Предположим, что x  V имеет два представления: x = x 1 + x 2 и x = y l + y 2. Отсюда x 1 + x 2 = = y l + y 2, или x 1 – y l = y 2 – x 2. Левая часть принадлежит V 1, а правая часть принадлежит V 2. Поскольку общим у V 1 и V 2 является 0, то x 1 = y l, x 2 = y 2.
V имеет два представления: x = x 1 + x 2 и x = y l + y 2. Отсюда x 1 + x 2 = = y l + y 2, или x 1 – y l = y 2 – x 2. Левая часть принадлежит V 1, а правая часть принадлежит V 2. Поскольку общим у V 1 и V 2 является 0, то x 1 = y l, x 2 = y 2.
Достаточность. Если для любого x  V верно единственное разложение x = = x 1 + x 2, то, по определению, V = V 1 + V 2. Покажем теперь, что единственным элементом, общим для V 1 и V 2, является 0. Действительно, если a
V верно единственное разложение x = = x 1 + x 2, то, по определению, V = V 1 + V 2. Покажем теперь, что единственным элементом, общим для V 1 и V 2, является 0. Действительно, если a 
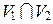 и a ¹ 0, то для x имеем два представления: x = x 1 + x 2 и x = (x 1 – a) + (x 2 + a), что противоречит единственности.¨
и a ¹ 0, то для x имеем два представления: x = x 1 + x 2 и x = (x 1 – a) + (x 2 + a), что противоречит единственности.¨
Определение 8.9. Обобщая определение 8.8, будем говорить, что пространство V разлагается в прямую сумму подпространств V 1, V 2,..., Vk, если
V = V 1 + V 2 +… + Vk; 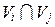 = 0 при
= 0 при 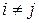 , где i, j = l, 2,..., k.
, где i, j = l, 2,..., k.
В этом случае любой вектор x 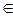 V единственным образом представляется в виде
V единственным образом представляется в виде
x = x 1 + x 2 +… + x k, x i  Vi, i = 1, 2,..., k.
Vi, i = 1, 2,..., k.
Например, в пространстве R n рассмотрим подпространства R 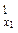 , R
, R 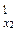 ,…, R
,…, R 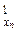 , порождаемые векторами вида (x 1, 0,..., 0), (0, x 2,..., 0),..., (0, 0,..., xn) соответственно. Поскольку x = (x 1, x 2,..., xn) = (x 1, 0,..., 0) + (0, x 2,..., 0) +... + (0, 0,..., xn), то R n = R
, порождаемые векторами вида (x 1, 0,..., 0), (0, x 2,..., 0),..., (0, 0,..., xn) соответственно. Поскольку x = (x 1, x 2,..., xn) = (x 1, 0,..., 0) + (0, x 2,..., 0) +... + (0, 0,..., xn), то R n = R 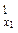 + R
+ R 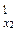 +… + R
+… + R 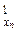 . Кроме того, R
. Кроме того, R 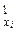
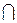 R
R 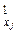 = 0 при всех i ¹ j, где i, j = l, 2,..., n, т. е. указанная сумма – прямая.
= 0 при всех i ¹ j, где i, j = l, 2,..., n, т. е. указанная сумма – прямая.
Теоремa 8.5. Если пространство V представлено в виде прямой суммы пространств V 1 и V 2, то dim V = dim V 1 + dim V 2.
Доказательство. Из соотношения V = V 1 + V 2 следует, что для любого x  V справедливо равенство x = x 1 + x 2, где x 1
V справедливо равенство x = x 1 + x 2, где x 1  V 1, x 2
V 1, x 2  V 2. Пусть u 1, u 2,..., u k – базис пространства V 1 (dim V 1 = k) и v 1, v 2,…, v r – базис пространства V 2 (dim V 2 = r). Тогда для x 1 и x 2 имеют место разложения x 1 =
V 2. Пусть u 1, u 2,..., u k – базис пространства V 1 (dim V 1 = k) и v 1, v 2,…, v r – базис пространства V 2 (dim V 2 = r). Тогда для x 1 и x 2 имеют место разложения x 1 =  u 1 +
u 1 +  u 2 +... +
u 2 +... + 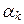 u k и x 2 =
u k и x 2 = 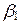 v 1 +
v 1 + 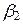 v 2 +... +
v 2 +... + 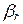 v r. Следовательно,
v r. Следовательно,
x = x 1 + x 2 =  u 1 +
u 1 +  u 2 +... +
u 2 +... + 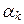 u k +
u k + 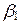 v 1 +
v 1 + 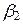 v 2 +... +
v 2 +... + 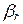 v r.
v r.
Поскольку 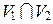 = 0, то векторы u 1, u 2,..., u k, v 1, v 2,…, v r линейно независимы (докажите это), и, согласно последнему равенству, эти векторы порождают все пространство V. Значит, они образуют базис V и dim V = k + r. ¨
= 0, то векторы u 1, u 2,..., u k, v 1, v 2,…, v r линейно независимы (докажите это), и, согласно последнему равенству, эти векторы порождают все пространство V. Значит, они образуют базис V и dim V = k + r. ¨
 2015-08-21
2015-08-21 2586
2586
