Во множестве линейных операторов, действующих из V в W, определим операции суммы операторов и умножения оператора на число.
Определение 10.10. Суммой линейных операторов A и B называется оператор A + B, определяемый равенством (A + B) x = Ax + Bx,  x
x  V.
V.
Определение 10.11. Произведением линейного оператора A на число a называется оператор a A, определяемый равенством (a A) x = a (Ax),  x
x  V.
V.
Линейность операторов A + B и a A очевидна.
Операторы A и B, действующие из V в W в заданных базисах, имеют мат-рицы А и В одинаковых размеров. Учитывая равенство (10.6), получаем матричные равенства (А + В) x = А x + В x, (aА) x = a (А x) для суммы операторов и произведения оператора на число, т. е. матрицей суммы операторов является сумма матриц этих операторов, а матрицей произведения оператора на число является произведение матрицы оператора на это число.
Определение 10.12. Пусть U, V и W – три линейных пространства размерностей k, n и т соответственно. Произведением, или композицией, двух линейных операторов A: V ® W и B: U ® V называется оператор C: U ® W, обозначаемый C = AB, такой, что
Cx = (AB) x = A (Bx),  x
x  U.
U.
Таким образом, произведение операторов A и B состоит в последовательном выполнении преобразований B и A, т. е. сначала на вектор x действует оператор B, а затем на полученный результат действует оператор A.
Линейность оператора C = AB вытекает из следующего равенства:
C ( x 1 +
x 1 +  x 2) = A (B (
x 2) = A (B ( x 1 +
x 1 +  x 2)) = A (
x 2)) = A ( Bx 1 +
Bx 1 +  Bx 2) =
Bx 2) =  A (Bx 1) + +
A (Bx 1) + +  A (Bx 2) =
A (Bx 2) =  (AB) x 1 +
(AB) x 1 +  (AB) x 2 =
(AB) x 2 =  Cx 1 +
Cx 1 +  Cx 2,
Cx 2,  x 1, x 2
x 1, x 2  U,
U, 
 ,
, 
 R.
R.
Покажем, что матрица произведения линейных операторов равна произведению матриц этих операторов. В самом деле, пусть u 1, u 2,…, u k – базис пространства U, v 1, v 2,…, v n – базис пространства V, w 1, w 2,…, w m – базис пространства W. Тогда, согласно равенству (10.3), имеем
(AB) u j = A (Bu j) = A 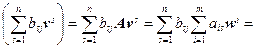
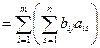 w i
w i 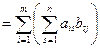 w i, j = 1, 2,..., k,
w i, j = 1, 2,..., k,
откуда следует справедливость сформулированного выше утверждения.
Заметим, что, вообще говоря, как и для матриц, AB 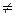 BA.
BA.
Пример 7. Из геометрических соображений ясно, что последовательное выполнение двух поворотов плоскости R 2 на углы j и y равносильно одному повороту ее на угол j + y.
Пусть A и B – операторы поворота на угол j и y соответственно, а
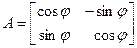 и
и 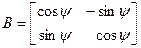 –
–
их матрицы. Тогда поворот на угол j + y осуществляет оператор с матрицей
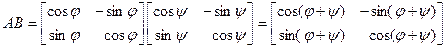 ,
,
откуда следует, что результирующий поворот осуществлен на угол j + y. ·
Справедливы следующие свойства линейных операторов:
1°. A + B = B + A.
2°. (A + B) + C = A + (B + C).
3°. A + О = A.
4°. A + ( – A) = O.
5°. 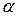 (
(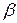 A) = (
A) = (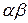 ) A,
) A, 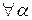 ,
, 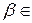 R.
R.
6°. (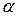 +
+ 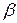 ) A =
) A = 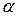 A +
A + 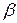 A,
A, 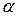 (A + B) =
(A + B) = 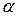 A +
A + 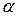 B,
B, 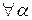 ,
, 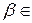 R.
R.
7°. 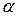 (AB) = (
(AB) = (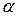 A) B,
A) B, 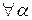
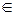 R.
R.
8°. (A + B) C = AC + BC.
9°. A (B + C) = AB + AC.
10°. (AB) C = A (BC).
Справедливость свойств 1°–6° очевидна. Докажем свойство 10°. Действительно, по определению произведения линейных операторов имеем
(A (BC)) x = A ((BC) x) = A (B (Cx));
((AB) C) x = (AB)(Cx) = A (B (Cx)).
Откуда и следует справедливость свойства 10°.
Свойства 7°–9° доказываются аналогично.
 2015-08-21
2015-08-21 5000
5000
