Глава 4. Линейные операторы
Тема 10. Линейные операторы и их матрицы
Понятие линейного оператора
Определение 10.1. Пусть V и W – два линейных пространства. Отображение A: V ® W, называется линейным оператором, если
A (a x 1 + b x 2) = a Ax 1 + b Ax 2,  x 1, x 2
x 1, x 2  V,
V,  a, b
a, b  R. (10.1)
R. (10.1)
Из определения линейного оператора следует более общее соотношение, которому он удовлетворяет:
A ( x 1+
x 1+  x 2+…+
x 2+…+ 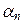 x n) =
x n) =  Ax 1+
Ax 1+  Ax 2+…+
Ax 2+…+ 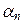 Ax n,
Ax n,
 x i
x i  V,
V, 
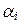
 R, i = 1, 2, …, n.
R, i = 1, 2, …, n.
Определение 10.2. Вектор y = Ax называется образом вектора x  V.
V.
Определение 10.3. Оператор, который каждому вектору x  V ставит в соответствие нулевой вектор 0
V ставит в соответствие нулевой вектор 0  W, является, очевидно, линейным и называется нулевым оператором. Нулевой оператор обозначается символом О. Таким образом, Оx = 0,
W, является, очевидно, линейным и называется нулевым оператором. Нулевой оператор обозначается символом О. Таким образом, Оx = 0,  x
x  V.
V.
Определение 10.4. Линейный оператор A, для которого Ax = x,  x
x  V, называется тождественным и обозначается Е.
V, называется тождественным и обозначается Е.
Определение 10.5. Оператор A, удовлетворяющий соотношению Ax = a x для некоторого фиксированного a  R, называется скалярным оператором, или оператором подобия. При a = – 1 оператор – A называется противоположным оператору A. Очевидно, при a = 0 и a = 1 скалярный оператор превращается в нулевой и тождественный соответственно.
R, называется скалярным оператором, или оператором подобия. При a = – 1 оператор – A называется противоположным оператору A. Очевидно, при a = 0 и a = 1 скалярный оператор превращается в нулевой и тождественный соответственно.
Определение 10.6. Областью значений, или образом, линейного оператора A: V ® W называется множество всех векторов вида y = Ax,  x
x  V, и обозначается im A (от англ. image – «образ»).
V, и обозначается im A (от англ. image – «образ»).
Таким образом,
im A = { y  W | y = Ax,
W | y = Ax,  x
x  V }.
V }.
Определение 10.7. Ядром линейного оператора A называется множество всех векторов x  V, для которых Ax = 0, и обозначается ker A (от англ. kernel – «ядро»):
V, для которых Ax = 0, и обозначается ker A (от англ. kernel – «ядро»):
ker A = { x  V | Ax = 0 }.
V | Ax = 0 }.
Легко убедиться, что образ im A линейного оператора A: V ® W является подпространством пространства W, а ядро ker A – подпространством пространства V. В самом деле, если y 1= Ax 1 и y 2= Ax 2, то в силу формулы (10.1) векторы A ( x 1 +
x 1 +  x 2) =
x 2) =  y 1 +
y 1 +  y 2,
y 2, 
 ,
, 
 R, принадлежат, очевидно, im A. Аналогично показывается, что ker A – подпространство пространства V.
R, принадлежат, очевидно, im A. Аналогично показывается, что ker A – подпространство пространства V.
Определение 10.8. Размерность образа im A линейного оператора называется рангом оператора и обозначается dim (im A), а размерность ядра ker A называется дефектом оператора и обозначается dim (ker A).
 2015-08-21
2015-08-21 1991
1991