Если A: R 2 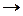 R 2 или A: R 3
R 2 или A: R 3 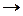 R 3 – линейный оператор, действующий в пространстве R 2 или R 3, то его матрица имеет вид
R 3 – линейный оператор, действующий в пространстве R 2 или R 3, то его матрица имеет вид
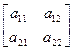 или
или 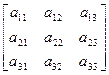
соответственно. Этот оператор переводит векторы из R 2 в векторы из R 2 или векторы из R 3 в векторы того же пространства R 3.
Рассмотрим несколько примеров.
Пример 1. Пусть A – оператор подобия, отображающий вектор x  R 3 в некоторый параллельный ему вектор y = a x. Линейность этого оператора очевидна.
R 3 в некоторый параллельный ему вектор y = a x. Линейность этого оператора очевидна.
Если i, j, k – базис пространства R 3, то
Ai = a i = a i + 0 j + 0 k = 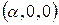 ;
;
Aj = a j = 0 i + a j + 0 k = 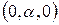 ;
;
Ak = a k = 0 i + 0 j + a k = 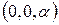 .
.
Значит, матрица этого оператора имеет вид
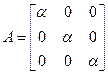 .
.
При 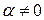 областью значений оператора подобия является, очевидно, все пространство R 3, а ядром – нулевой вектор, т. к. только этот вектор удовле-творяет при преобразовании подобия равенству Ax = 0. Ясно, что ранг оператора подобия dim (im A) = 3, а его дефект dim (ker A) = 0.·
областью значений оператора подобия является, очевидно, все пространство R 3, а ядром – нулевой вектор, т. к. только этот вектор удовле-творяет при преобразовании подобия равенству Ax = 0. Ясно, что ранг оператора подобия dim (im A) = 3, а его дефект dim (ker A) = 0.·
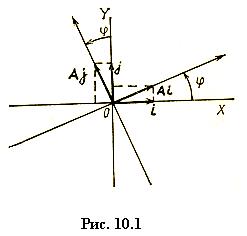
Пример 2. Пусть A – поворот векторов плоскости R 2 вокруг начала координат на угол j против часовой стрелки. Это преобразование линейно, т. к., если векторы a и b сначала сложить и затем повернуть их сумму a + b на угол j, или, если оба вектора a и b повернуть сначала на угол j и затем их сложить, то получим тот же результат. Аналогично, не имеет значения, умножить ли вектор a на число a, а затем повернуть его на угол j или сделать это в обратном порядке.
Найдем матрицу оператора поворота. Для этого обратимся к рис. 10.1, из которого видно, что
Ai = 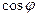 i +
i + 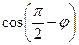 j =
j = 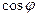 i +
i + 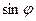 j;
j;
Aj = 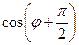 i +
i + 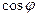 j = –
j = – 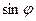 i +
i + 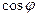 j.
j.
Так что искомая матрица оператора поворота в базисе i, j имеет вид
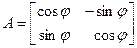 .
.
 |
Используя матрицу оператора, получим формулы преобразования координат вектора на плоскости при повороте ее на угол j – так называемые формулы преобразования поворота. Пусть x = 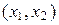 – вектор на плоскости, тогда координаты у 1, у 2 вектора Ax при повороте плоскости на угол j определяются из соотношений
– вектор на плоскости, тогда координаты у 1, у 2 вектора Ax при повороте плоскости на угол j определяются из соотношений
y = А x 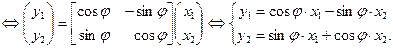
Ясно, что областью значений оператора поворота является вся плоскость R 2, а ядром – нулевой вектор, т. е. dim (im A) = 2, dim (ker A) = 0.·
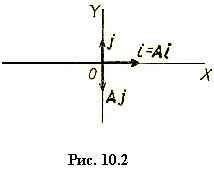
Пример 3. Пусть A – зеркальное отражение (симметрия) векторов плоскости R 2 относительно оси Ox. Линейность такого преобразования очевидна. Из рис. 10.2 следует, что Ai = i = 1 i + 0 j, Aj = – j = 0 i – 1 j, поэтому матрица данного оператора имеет вид
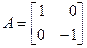 .·
.·
 |
Пример 4. Пусть A – зеркальное отражение векторов пространства R 3 относительно плоскости Oxy. При этом Ai = i, Aj = j, Ak = – k, так что матрица данного оператора имеет вид
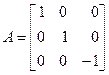 .
.
Очевидно, что im A = R 3, а ker A = { 0 }.·
Пример 5. Пусть A – ортогональное проектирование векторов пространства R 3 на плоскость Oxy. Линейность этого отображения следует из линейных свойств проекций векторов. Так как при этом имеем Ai = i, Aj = j, Ak = 0, то матрица данного оператора имеет вид
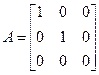 .
.
Очевидно, в этом случае областью значений оператора является плоскость Oxy, а ядром его служат все векторы, перпендикулярные этой плоскости, так что dim (im A) = 2, dim (ker A) = 1.·
Пример 6. Пусть A: R 3® R 2 – линейный оператор, для которого Ax = y, где
y = 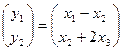 , x =
, x = 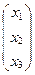 .
.
Найти матрицу оператора A в базисах i, j, k пространства R 3 и i, j пространства R 2.
Решение. Согласно условию, матрица А имеет две строки и три столбца:
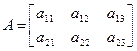 .
.
По определению,
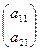 = Ai =
= Ai = 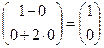 ;
; 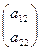 = Aj =
= Aj = 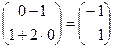 ;
; 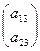 = Аk =
= Аk = 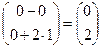 .
.
Так что
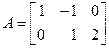 .·
.·
 2015-08-21
2015-08-21 22045
22045
