Обратный оператор

Определение 10.13. Линейный оператор A называется невырожденным, если его ядро состоит только из нулевого вектора, т. е. Ax = 0 Û x = 0, в противном случае оператор называется вырожденным, т. е. для вырожденного оператора равенство Ax = 0 возможно и при некотором x 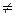0.

Оператор проектирования из примера 5, очевидно, является вырожденным, т. к. он переводит ненулевые векторы, ортогональные плоскости Oxy, в нулевой вектор. Невырожденными являются, например, операторы подобия при 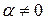и поворота.

Из определения невырожденного оператора следует, что его дефект равен нулю, т. е. dim (ker A) = 0.

Важнейшим свойством невырожденного оператора является взаимная однозначность отображения. Итак, если A: V ® W – невырожденный оператор, то для каждого y 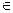W существует единственный x V, такой, что y = Ax.

Определение 10.14. Оператор, определяющий вектор x для данного y из соотношения y = Ax, называется обратным оператору A и обозначается A ^–1, т. е. x = A ^–1 y.

Таким образом, исходя из определения обратного оператора, имеем

x = A ^–1 y = A ^–1(Ax) = (A ^–1 A) x, x V.

Аналогично,

y = Ax = A (A ^–1 y) = (AA ^–1) y, y W.

Из этих равенств видно, что

A ^–1 A = AA ^–1 = Е, (10.7)

где Е – тождественный оператор.

Докажем линейность обратного оператора. Пусть y ¹и y ²– произвольные векторы из W и x ¹и x ² – отвечающие им единственные векторы из V, для которых y ¹= Ax ¹, y ²= Ax ². Тогда, учитывая линейность оператора A, получим

A ^–1( y ¹+ y ²) = A ^–1( Ax ¹+ Ax ²) = A ^–1(A ( x ¹+ x ²)) =

= (A ^–1 A)( x ¹+ x ²) = x ¹+ x ²= A ^–1 y ¹+ A ^–1 y ², , R.

Легко проверить, что если линейные операторы A и B невырожденные, то и их произведение AB является невырожденным оператором, обратным для которого служит B ^–1 A ^–1, т. е.

(AB)^–1 = B ^–1 A ^–1.

Это следует из равенств

(AB)(B ^–1 A ^–1) = A (B (B ^–1 A ^–1)) = A ((BB ^–1) A ^–1) = AEA ^–1 = AA ^–1 = E;

(B ^–1 A ^–1)(AB) = B ^–1(A ^–1(AB)) = B ^–1((A ^–1 A) B) = B ^–1 EB = B ^–1 B = E.

Пусть u ¹, u ²,…, u ⁿ – фиксированный базис пространства V и A: V ® V – невырожденный линейный оператор. Тогда в этом базисе линейным операторам A и A ^–1 соответствуют единственные квадратные матрицы А и А ^–1 порядка n, которые, согласно равенствам (10.7), удовлетворяют соотношению