2015-08-21
630
Рассматриваются игры двух лиц с нулевой суммой. Игрок А располагает p чистыми стратегиями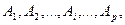 
а игрок В соответственно q чистыми стратегиями 
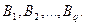Первый игрок может выбрать любую стратегию 
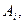второй игрок может выбрать любую стратегию 
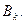В этом случае игра считается сыгранной, и ее результат выражается некоторым числом («платежом»), который обозначим через 
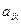и будем называть его «выигрышем» игрока А. Игра с «нулевой суммой» означает, что при этом «выигрыш» игрока В составит 
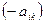(числа 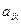могут быть и отрицательными). Матрица 
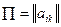порядка 
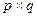называется платежной матрицей или матрицей игры.
Таблица 1.1
| 
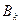
| Стратегии игрока В |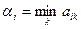 
| ||||
| … |
| … | 
| |||
| 
| … | 
| … | 
| 
| |
|
| … |
| … |
|
| |
|
| 
| … |
| … | 
| 
| |
|
|
| … |
| … |
|
| |
| 
| … | 
| … | 
| 
| |
| 
| … | 
| … | 
| 
| 
|
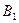
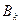
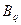
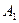
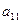
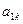
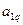
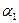
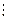
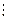
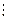
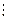
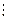
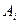
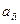
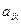
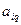
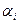
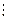
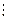
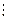
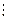
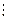
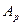
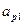
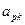
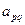
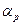
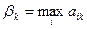
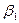
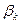
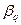
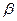
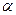
Числа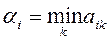 
и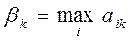 
указывают минимально гарантированный выигрыш для игрока А, применяющего стратегию 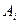, и максимально «гарантированный» проигрыш игроком В при использовании им стратегии .
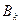Величина
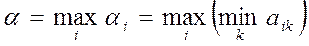(1.1)
называется нижней ценой игры, максимальным выигрышем А, или коротко максимином, а соответствующая ему стратегия (строка) – максиминной. Аналогично
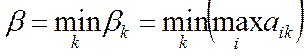(1.2)
называется верхней ценой игры, минимаксным проигрышем В, или минимаксом, а соответствующая стратегия (столбец) игрока В – минимаксной. Всегда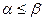 
. Принцип, согласно которому игроки выбирают эти стратегии, называется принципом максимина (для А) или минимакса (для В).
Если игрок А выбирает свою максиминную стратегию, то при любой стратегии, выбираемой игроком В, ему обеспечивается выигрыш не менее, чем 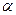. Аналогично для игрока В, при выборе им стратегии, при которой достигается 
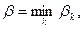обеспечивается выигрыш (или выигрыш игрока А) не более, чем .
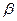Если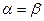 
, то говорят, что игра, определяемая матрицей 
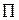, имеет седловую точку, а общее значение 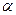и 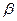, которое будем обозначать через 
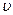- ценой игры.
В этом случае оптимальным решением игры для обоих игроков является выбор максиминной (для А) и минимаксной (для В) стратегий. Любое отклонение для каждого игрока от этих стратегий не может оказаться выгодным.
