Расчет средних показателей способом моментов

Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчетов средней можно упростить и облегчить, если воспользоваться ее свойствами:

1. если все индивидуальные значения признака (все вварианты) уменьшить в i раз, то среднее значение нового признака соответственно уменьшится или увеличитсяв i раз.

2. Если вес варианты осредняемого признака уменьшить на число А, то средняя арифметическая соответственно увеличится на это же число А.

3. Если веса всех осредняемых вариантов уменьшить или увеличить в К раз, то средняя арифметическая не изменится.

В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве i – величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отчета, поэтому такой метод вычисления средней называется “способом отчета от условного нуля” или “способом моментов”.

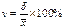Допустим, что все варианты X сначала уменьшены на одно и то же чило А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов x.

Тогда новые варианты будут выражаться,

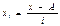
а их новая средняя арифметическая

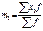
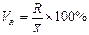m ₁ – момент первого порядка- формулой и будет равна средней из первоначальных вариантов, уменьшенной сначала на А, а затем в i раз, т.е.

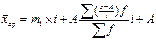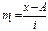
Для получения действительной средней надо момент первого порядка m ₁ умножить на i и прибавить А.

Данный способ вычисления средней арифметической из вариционного ряда называют «способом моментов». Применяется этот способ в рядах с равными интервалами.