Доказательство

1. Для пифагоровых троек условие 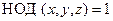влечет

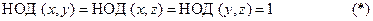
В самом деле, если, например, 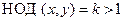, то 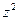делится на 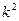в силу того, что 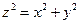, т. е. z делится на k, или 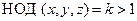, что противоречит условию.

2. Для любой примитивной пифагоровой тройки 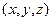числа x, y разной четности. Действительно, x и y не могут быть оба четными в силу (*). Если x и y оба нечетные, т. е.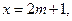 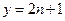, то 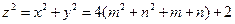, т. е. 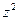делится на 2, но не на 4. Итак, 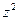четно, тогда z тоже четно (см. с. 121), т. е. 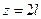, значит, 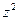делится на 4. Получили противоречие.

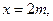
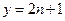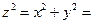
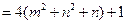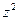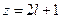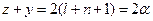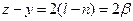3. Положим для определенности . Тогда т. е. нечетно и, следовательно, z нечетно, т. е. . Тогда и , следовательно, .

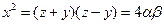4. Покажем, что α и β взаимно простые числа разной четности.

а) Пусть 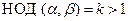, т. е.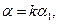 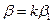. Тогда

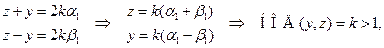
что противоречит (*).

б) Пусть 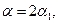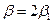. Тогда

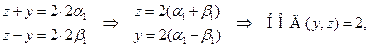
что противоречит (*).

в) Аналогично доказывается, что α и β одновременно не могут быть нечетными.

5. Итак, 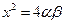, тогда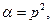 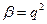, причем 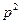и 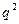взаимно простые числа разной четности. Но тогда p и q также являются взаимно простыми числами разной четности, причем

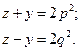
Отсюда легко находим: .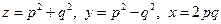

Теорема доказана. Ясно, что при 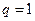(1.2.5) переходит в (1.2.4). Решение (1.2.5) при любых натуральных 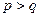дает всевозможные пифагоровы тройки без учета их примитивности. Оно было хорошо известно в античную эпоху и указано в таких великих книгах древности, как «Начала» Евклида (III в. до н. э.) и «Арифметика» Диофанта (III в. н. э.). На этом можно было бы поставить точку, но...

Около 1630 г. скромный юрист из французского города Тулузы Пьер Ферма (1601 — 1665), проводивший свободное от работы время в математических упражнениях, на полях «Арифметики» Диофанта против того места, где Диофант решает задачу Пифагора, сделал запись: «Наоборот, невозможно разложить куб на два куба или биквадрат на два биквадрата и вообще никакую степень выше второй нельзя разложить на сумму двух степеней с теми же показателями. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки».

Так, на полях Диофантовой «Арифметики» Ферма сформулировал утверждение, вошедшее в историю математики как великая теорема Ферма: для любого натурального 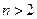уравнение

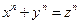
не имеет решений в целых положительных числах x, y, z.

Однако общее доказательство теоремы, обещанное Ферма, бесследно исчезло: вместо него в бумагах Ферма было найдено лишь частное доказательство для случая 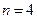. Не нашли это доказательство и поныне лучшие математические умы мира.

Прошло более 350 лет, в течение которых предпринимались героические усилия для доказательства коварной теоремы. В 1770 г. Л. Эйлер доказал теорему для 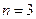, в 1825 г. П. Дирихле и А. Лежандр — для 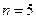в 1839 г. Г. Ламе — для 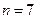. Затем Э. Куммер наметил общий подход к проблеме и доказал теорему для всех простых чисел n из промежутка [3; 100]. Страсти вокруг теоремы Ферма накалялись. В 1907 г. за ее доказательство была объявлена международная премия в 100 000 немецких марок. Теорема Ферма стала каким-то математическим наваждением.

К настоящему времени с помощью ЭВМ установлено, что 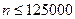. Последняя сенсация облетела математический мир в 1993 г.: английский математик Эндрю Уайлс из Пристонского университета в докладе, сделанном в Институте математических наук имени Исаака Ньютона Кембриджского университета перед 75 виднейшими математиками мира, представил доказательство теоремы Ферма. Время покажет: будет ли в нем обнаружена ошибка, как и в великом множестве предыдущих доказательств, или нет.

Тем не менее, все эти поиски и прежде всего идеи российского математика А. Паршина нельзя назвать бесполезными. Они породили массу новых плодотворных направлений в математике и, таким образом, необычайно обогатили саму математику.

Так, начатое Пифагором во времена, когда человечество знало лишь натуральные числа, исследование «безобидного» уравнения

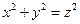
привело к сложнейшей проблеме современной теории чисел — исследованию в целых числах уравнения

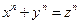
— великой и неприступной на протяжении четырех столетий теореме Ферма.

ТАБЛИЦА ПИФАГОРА

Кроме теоретической арифметики, ставшей фундаментом современной теории чисел и оставившей ей ряд нерешенных проблем, была у пифагорейцев и другая ветвь арифметики, более близкая современному значению слова, — учение о правилах действия над числами. Этот раздел арифметики назывался у пифагорейцев логистикой (Λογιστικμ — счетное искусство). В состав логистики входили арифметические действия с натуральными числами вплоть до извлечения квадратных и кубических корней, действия с дробями, техника вычислений на счетной доске. Хотя задачи вычислительной арифметики отвечали насущным потребностям жизни — торговле, строительству, расчету метательных орудий, логистика (искусство вычислять) по сравнению с арифметикой (наукой о числах) считалась пифагорейцами наукой второго сорта и развивалась весьма слабо.

Как и в теоретической арифметике, числа-камешки играли в логистике значительную роль. Они успешно использовались в первой в истории человечества «вычислительной машине» — абаке. Абак выглядел просто: это была разлинованная плита, в каждой колонке которой камешки имели разные значения: единицы, десятки, сотни и т.д. Сегодня так до конца и не выяснено, откуда произошло слово «абак»: его греческое толкование неговорящий (’Α-βακής — бессловесный), возможно, указывает на молчаливый характер процесса счета, а семитическое — означает дощечка, покрытая слоем пыли. Трудно сказать, где появился первый абак — в Древнем Египте, Древней Греции или Древнем Китае. Ясно лишь, что китайская модель абака — суаньпань — в виде бусинок, нанизанных на прутики, оказалась наиболее практичной и встречается даже в наш век электронных микрокалькуляторов.

Как бы то ни было, в V в. до н. э., по свидетельству Геродота, абак был хорошо известен и в Греции, и в Египте и отличался лишь направлением перекладывания камешков. О популярности абака говорит и отрывок из «Истории» древнегреческого историка Полибия (ок. 201 — ок. 120 до н. э.): «Придворные — как камешки на счетной доске: захочет счетчик, и они будут стоить один халк, а захочет — так и целый талант».

В 1848 г. при раскопках на острове Саламин был найден мраморный абак огромных размеров (1,5 ´ 0,75 м). Расшифровка надписи на мраморной доске позволила воспроизвести способ пользования абаком (рис. 38). Если пронумеровать все 10 колонок справа налево (именно так передвигали камешки греки), то в первых 8 колонках каждый камешек соответственно обозначал 1, 5, 10, 50, 100, 500, 1000, 5000 драхм (драхма и талант — денежные единицы в Греции; 1 талант = 6000 драхм). Последние две колонки служили для подсчета числа талантов.

Рис. 38. Мраморный абак, найденный на острове Саламин. IV в. до н. э. (?) Афины. Национальный музей.

Но подсчитанные числа необходимо было запомнить, лучше записать. Так появляется письменное фиксирование чисел — нумерация, а затем и письменный счет. Надо сказать, что греческая нумерация была шагом назад по сравнению с вавилонской. Обе ее разновидности — аттическая и ионийская — не были позиционными, и в этом был их главный недостаток. Аттическая нумерация (очень похожая на римскую) была со временем вытеснена более компактной ионийской, которую мы и рассмотрим коротко. В основу ионийской нумерации положены все 24 буквы греческого алфавита и три архаические финикийские буквы (Fς — вау, TϠ — сампи и 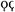— коппа). Числовые значения этих 27 знаков показаны в таблице, откуда также ясно, что с их помощью можно было изобразить все числа от 1 до 999. Например: ια = 11, ρβ = 102, φξγ = 563 и т. д. Чтобы отличать буквы-слова от букв-чисел, над последними ставилась черта (поскольку нам путаница не грозит, мы черту опускаем).

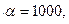
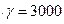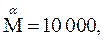
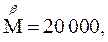
Для обозначения тысяч применялся штрих слева внизу буквы, например . Десятки тысяч обозначались знаком Μ с соответствующей буквой сверху, например 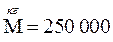. Запись чисел свыше 1000 можно рассматривать как зачатки позиционной системы счисления, окончательный переход к которой в Греции так и не был осуществлен.

Заметим, что алфавитная ионийская система нумерации была целиком воспринята в России с той лишь разницей, что греческие буквы были заменены сходными по начертанию буквами кириллицы. Лишь в конце XVII в. вместе с реформами Петра I в России стала вводиться так называемая арабская нумерация, ставшая сегодня международной.

Непозиционная ионийская система счисления делала письменный счет весьма громоздким. Так, чтобы умножить два числа, их представляли в виде суммы чисел вида (1.3.1), которые затем перемножались и складывались. Например:

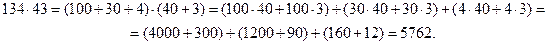
Вот как это выглядело бы в античном оригинале (справа дан «перевод» в арабскую нумерацию)[38]:

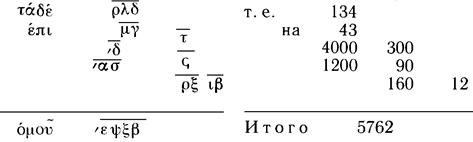
Для вычисления промежуточных результатов (т. е. для перемножения чисел вида (1.3.1) составлялись таблицы умножения. Такие таблицы были известны грекам издревле, и их изобретение приписывалось герою Троянской войны Паламеду — тому самому Паламеду, который разоблачил хитроумного Одиссея, прикинувшегося сумасшедшим, чтобы не идти на Троянскую войну.

Таблицы Паламеда были весьма громоздкими, ибо помимо сомножителей 1, 2,..., 9, которые составляют современную таблицу умножения — таблицу Пифагора, они должны содержать сомножители 10, 20,...., 90; 100, 200,..., 900 и т. д. Известны таблицы, составленные для 37 ´ 37 сомножителей от α до :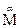

Таблицы содержали три столбца: множимое, множитель и произведение; они учитывали закон коммутативности умножения, и фактически в них было не 37 ´ 37 членов, а 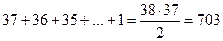. Фрагмент такой таблицы умножения, написанной на восковой доске безвестным древнегреческим школьником, хранится сегодня в Британском музее.

Ну а где же таблица Пифагора? Ее мы находим именно такой, какой привыкли видеть на обложке тетрадки в клеточку, в сочинении «Введение в арифметику» неопифагорейца Никомаха Геразского[39] (I — II вв.). Трактат Никомаха — наиболее полное из сохранившихся изложений пифагорейской арифметики. Несмотря на то, что Никомах жил четырьмя столетиями позже Евклида, его сочинение выглядит гораздо примитивнее арифметических книг (VII — IX книги) Евклидовых «Начал». Именно в сочинении Никомаха каким-то чудом сохранилась в первозданном виде вся аура пифагорейского учения о числе со всей ее мистикой, пространными рассуждениями о божественном назначении чисел и т. д.

Итак, перед нами таблица Пифагора:

Разумеется, Никомах утверждает, что эта таблица, как и все в его книге, восходит к самому Пифагору. Но если это даже и так, то, как легко видеть из рассмотренного примера, античному вычислителю было мало толку от этой таблицы. По ней он смог бы найти произведение сомножителей не больших 10. Например: δ · γ = ιβ (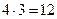). Для остальных произведений ему необходимы были более подробные таблицы. В таблице Пифагора только 55 неравных членов — это менее чем 1/12 часть от тех 703 произведений, которые фигурировали в таблицах Паламеда.

Как таблица умножения таблица Пифагора стала эффективной лишь с изобретением десятичной позиционной системы счисления, когда все умножение свелось к умножению целых чисел от 1 до 9. Разумеется, произошло это не вдруг. В XV в. в Европе разгорелась борьба между «абацистами» — защитниками старой счетной доски и «алгоритмиками» — приверженцами новой позиционной системы и новой индийской («арабской») нумерации.

На старинной гравюре XVI в. мы видим аллегорическое изображение этой борьбы: справа сидит Пифагор, считавшийся изобретателем абака, а слева — Боэций — римский философ VI в., которому в средневековой Европе приписывали изобретение новых цифр (рис. 39). Суд в споре Пифагора и Боэция призвана вершить сама Арифметика, стоящая за ними. Однако выражение лица Пифагора отнюдь не оптимистично, и, видимо, как честный ученый, он готов признать Боэция победителем.

Рис. 39. «Абацист» Пифагор (справа) и «алгоритмик» Боэций (слева). Гравюра из книги XVI в.

Итак, по существу, имя Пифагора в названии таблицы умножения отражает скорее дань уважения основоположнику логистики (арифметики), хотя по форме сегодняшняя таблица целиком скопирована с греческого оригинала.

Что касается таблицы Пифагора, приведенной у Никомаха, то скорее всего она была задумана не как таблица умножения, а как таблица, иллюстрирующая свойство пропорциональности чисел.

В самом деле, легко видеть, что любые две строки этой таблицы представляют собой набор чисел, находящихся в одинаковых отношениях друг к другу, т. е. пропорциональных. Таким образом, таблица Пифагора приводит нас к новой странице пифагорейской арифметики — учению о пропорциях.