Числа древними греками, а вместе с ними Пифагором и пифагорейцами мыслились зримо, в виде камешков[37], разложенных на песке или на счетной доске — абаке. По этой причине греки не знали нуля, так как его невозможно было «увидеть». Но и единица еще не была полноправным числом, а представлялась как некий «числовой атом», из которого образовывались все числа. Пифагорейцы называли единицу «границей между числом и частями», т. е. между целыми числами и дробями, но в то же время видели в ней «семя и вечный корень». Число же определялось как множество, составленное из единиц. Особое положение единицы как «числового атома» роднило ее с точкой, считавшейся «геометрическим атомом». Вот почему Аристотель писал: «Точка есть единица, имеющая положение, единица есть точка без положения». Итак, пифагорейские числа в современной терминологии — это натуральные числа.
Числа-камешки раскладывались в виде правильных геометрических фигур, эти фигуры классифицировались. Так возникли числа, сегодня именуемые фигурными:
линейные числа (т. е. простые числа) — числа, которые делятся только на единицу и на самих себя и, следовательно, представимы в виде последовательности точек, выстроенных в линию:
 (линейное число 5);
(линейное число 5);
плоские числа — числа, представимые в виде произведения двух сомножителей:
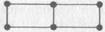 (плоское число 6);
(плоское число 6);
телесные числа, выражаемые произведением трех сомножителей:
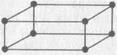 (телесное число 8);
(телесное число 8);
треугольные числа:
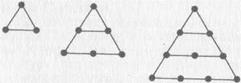 (треугольные числа 3, 6, 10);
(треугольные числа 3, 6, 10);
квадратные числа:
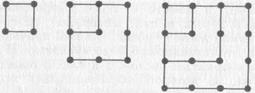 (квадратные числа 4, 9, 16);
(квадратные числа 4, 9, 16);
пятиугольные числа:
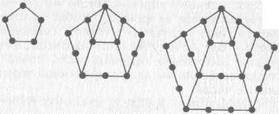 (пятиугольные числа 5, 12, 22)
(пятиугольные числа 5, 12, 22)
и т.д. Именно от фигурных чисел пошло выражение: «Возвести число в квадрат или куб».
Представление чисел в виде правильных геометрических фигур помогало пифагорейцам находить различные числовые закономерности. Например, чтобы получить общее выражение для n -го треугольного числа, которое есть не что иное, как сумма n натуральных чисел 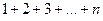 , достаточно дополнить это число до прямоугольного числа
, достаточно дополнить это число до прямоугольного числа 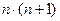 и увидеть (именно увидеть глазами!) равенство
и увидеть (именно увидеть глазами!) равенство
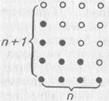
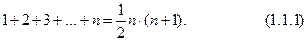
Написав последовательность квадратных чисел, опять-таки легко увидеть глазами выражение для суммы n нечетных чисел:

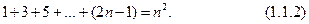
Наконец, разбивая n -е пятиугольное число на три 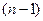 треугольных (после чего остается еще n «камешков»), легко найти его общее выражение:
треугольных (после чего остается еще n «камешков»), легко найти его общее выражение:
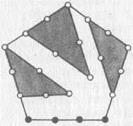
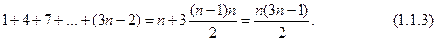
Разбиением на треугольные числа получается и общая формула для n -го k -угольного числа:
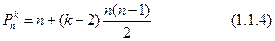
откуда при 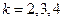 следуют формулы (1.1.1 — 1.1.3).
следуют формулы (1.1.1 — 1.1.3).
Конечно, сегодняшний школьник легко заметит, что суммы (1.1.1 — 1.1.3) есть не что иное, как арифметические прогрессии, разность которых d соответственно равна 1, 2, 3 (для k -угольного числа 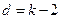 ), и по соответствующей формуле найдет эти суммы и общую формулу (1.1.4):
), и по соответствующей формуле найдет эти суммы и общую формулу (1.1.4):
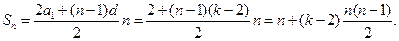
Но в том-то и прелесть пифагорейских доказательств, что они не требуют никаких предварительных знаний и в буквальном смысле очевидны. (Не отсюда ли пошло это столь любимое математиками слово?)
Заметим, что при выводе равенства (1.1.2) был использован излюбленный пифагорейцами метод гномона. Гномоном (Γνωμων — знаток, толкователь) пифагорейцы называли число или фигуру (черные точки в (1.1.2)), которая, будучи приложенной к основной фигуре (белые точки), сохраняет ее форму. Первоначально гномоном (буквально тот, кто знает) греки называли солнечные часы — прибор, позволявший по линиям, которые пересекает тень от вертикального столбика, разделять беспредельность времени на зримые части. Впоследствии число и стало для пифагорейцев таким гносеологическим гномоном, дававшим возможность различать вещи и тем самым овладевать ими в сознании. Методом гномона растут все живые организмы, что позволяет им сохранять свою индивидуальную форму.
Фигурное представление чисел помогало пифагорейцам открывать законы арифметических операций, а также легко переходить к числовой характеристике геометрических объектов — измерению площадей и объемов. Так, представляя плоское число 10 в двух формах:

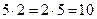
легко «увидеть» переместительный закон умножения:
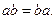
В том же числе 10:
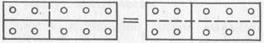
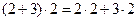
можно «разглядеть» и распределительный закон сложения относительно умножения:
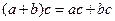
и т. д.
Наконец, если «камешки», образующие фигурные числа, мыслить в виде равных по площади квадратиков, то, укладывая их в прямоугольное число ab:
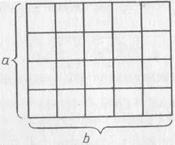
мы автоматически получаем формулу для вычисления площади прямоугольника: 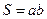 .
.
Важнейшей частью пифагорейской арифметики было учение о четных и нечетных числах. Не случайно Платон в своих диалогах неоднократно определял арифметику как «учение о четном и нечетном». Четное и нечетное были для пифагорейцев не только основными понятиями теории чисел, но и важнейшими философскими категориями. Пара четное — нечетное наряду с такими парами, как предел — беспредельное, мужское — женское, доброе — злое, включалась в 10 пар противоположностей, которые пифагорейцы считали началами всего сущего.
Исследователи Евклида давно обратили внимание на конец IX книги его «Начал» (предложения 21 — 34), который явно выпадал из общего контекста книги и выделялся своей архаичностью. Сегодня ни у кого не вызывает сомнения, что эта часть «Начал» есть не что иное, как целиком воспроизведенный фрагмент древнего пифагорейского учения о четном и нечетном.
Мы не будем приводить здесь все 14 предложений о четном и нечетном, а отметим лишь их основной результат, который можно сформулировать так: произведение двух чисел четно тогда и только тогда, когда по крайней мере один из сомножителей четен. Этой теореме суждено было сыграть кардинальную роль во всем пифагорейском учении, ибо именно на нее опиралось доказательство знаменитой теоремы о несоизмеримости, которую мы рассмотрим на с. 141.
Вершиной пифагорейского учения о четном и нечетном является последнее предложение IX книги «Начал» Евклида — предложение 36, посвященное совершенным числам. Совершенным называется натуральное число, равное сумме всех своих правильных (т. е. меньших этого числа) делителей. Например:
6 = 1 + 2 + 3;
28 = 1 + 2 + 4 + 7 + 14;
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248.
Предложение 36 утверждает, что если сумма
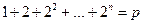
является простым числом, то число 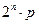 будет совершенным.
будет совершенным.
Поскольку ясно, что правильными делителями числа 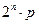 будут числа
будут числа
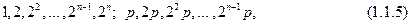
то доказательство предложения 36 сводится к доказательству двух утверждений:
1) других делителей, кроме (1.1.5), у числа 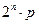 нет;
нет;
2) сумма делителей равна самому числу, т. е.
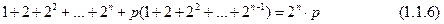
Первое утверждение доказывается с помощью учения о четном и нечетном (предложения 21 — 34). А вот второе доказательство легко провести на «камешках».
В самом деле, так как по условию 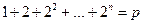 , то, сокращая в (1.1.6) обе части равенства на p, имеем
, то, сокращая в (1.1.6) обе части равенства на p, имеем
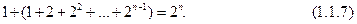
Теперь изобразим данную сумму фигурными числами:
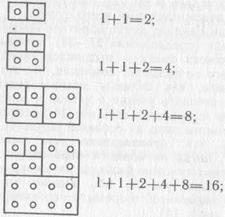
откуда легко «усмотреть» равенство (1.1.7).
Учитывая (1.1.7), получим компактную форму записи совершенного числа 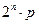 :
:
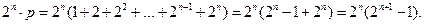
Итак, число

является совершенным при тех значениях n, при которых число 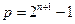 является простым.
является простым.
Легко найти первые подходящие значения n:
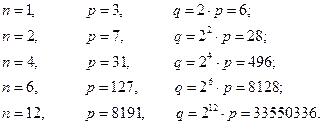
Первые четыре совершенных числа были известны пифагорейцам.
А есть ли другие совершенные числа, кроме чисел вида (1.1.8), найденных пифагорейцами? Этот вопрос вот уже 2500 лет, увы, остается открытым. Ясно, что совершенные числа вида (1.1.8) являются четными. Лишь в XVIII в. великий Эйлер доказал, что никаких других четных совершенных чисел нет. Однако до сих пор не известно ни одного нечетного совершенного числа и вопрос об их существовании все еще ждет своего решения. На сегодня лишь известно, что нечетных совершенных чисел в промежутке 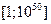 нет. Четных совершенных чисел на сегодня найдено 27, наибольшее из них равно
нет. Четных совершенных чисел на сегодня найдено 27, наибольшее из них равно 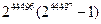 .
.
Не правда ли, удивительно, как в, казалось бы, невинной забаве с раскладыванием камешков на песке древние пифагорейцы сумели отыскать математическую проблему, которая и по сей день остается нерешенной?! И просто поражает интуиция пифагорейцев, нашедших задолго до нашей эры единственную (пока или навсегда?!) формулу для совершенного числа!
 2015-09-06
2015-09-06 2957
2957








