Диференціальні рівняння першого порядку. Основні поняття та означення

Диференціальне рівняння першого порядку в загальному випадку можна записатиу виглядіF(x, y, y^l) = 0,(1)

де x – незалежна змінна, y – невідома функція від x, F(x, y, y^l) – задана функція змінних x, y, y^l = .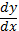

Якщо рівняння (1) можна розв’язати відносно похідної, то його записуватимемо у вигляді y^l = f(x, y). (2)

Таку форму запису диференціального рівняння називають нормальною. Найпростішим з диференціальних рівнянь у нормальній формі є рівняння y^l = f(x). Якщо функція f(x) визначена і неперервна на деякому інтервалі (a, b), то, як відомо з математичного аналізу, y = 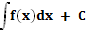, де C – довільна стала.

У багатьох випадках рівняння (2.2) зручно записувати як 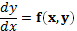або у вигляді

dy − f(x, y)dx = 0, який є окремим випадком рівняння

M(x, y)dx + N(x, y)dy = 0, (3)

де M(x, y), N(x, y) – відомі функції (коефіцієнти рівняння).

Рівняння (3) зручне тим, що змінні x і y у ньому рівноправні, тобто кожну з них можна розглядати як функцію від іншої.

Розв’язком диференціального рівняння (2) на інтервалі (a, b) називають неперервно диференційовну на цьому інтервалі функцію y = y(x), яка перетворює рівняння (2) у тотожність, тобто

y^l ≡ f(x, y(x)).

Розв’язок рівняння (2.2) може бути заданий не тільки явно, тобто як y = y(x), але й у неявному вигляді Φ(x, y) = 0 (у вигляді, не розв’язаному відносно y) або у параметричній формі: x = 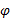(t), y = ψ(t).