Система звич.ДР. Основні поняття

Сукупністьспiввiдношень вигляду

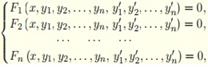(1)

де y1, y2,..., yn – шуканiфункцiї незалежної змiнної x, називають системою звичайних диференцiальнихрiвняньпершого порядку.

Якщо (1) можна розв’язати вiдноснопохiднихусiхфункцiй, то одержимо систему

яку називають нормальною.

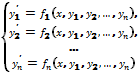(2)

Розв’язком системи (2) на деякому iнтервалi (a, b) називають впорядковану сукупнiстьфункцiй y1 = y1(x), y2 = y2(x),..., yn = yn(x), (3) визначених i неперервнодиференцiйовних на цьому iнтервалi, якщо вона кожне рiвняння системи (2) перетворює у тотожнiсть, яка справджується для

всiх значень x ∈ (a, b). Кривув (n + 1)-вимiрномупросторi (x, y1, y2,..., yn), яка вiдповiдає розв’язку (3), називають iнтегральною кривою системи(2).

Задача Кошi для системи (2) формулюється так: серед усiхрозв’язкiвцiєї системи знайти розв’язок (3), який задовольняє умови

y1(x0) = y10, y2(x0) = y20,..., yn(x0) = yn0, (4)

де x=x0 – деяка точка з iнтервалу (a, b), а y10, y20,..., yn0 – довiльнiзаданiдiйснi числа.

Сукупнiсть чисел x0, y10, y20,..., yn0 називають початковими даними системи (2), а умови (4) –початковими умовами системи (2). Для iснуваннянеперервнодиференцiйовного розв’язку задачiКошi (2), (4) досить припустити,щоб правi частини системи (2) були неперервними в деякому околi початкових даних (теорема Пеано). Наступна теорема гарантує iснування єдиного розв’язку задачiКошi (2),(4).

Теорема (Кошi). Нехай правi частини системи (2) визначенi в (n + 1)-вимiрномупаралелепiпедi

G ={(x, y1, y2,..., yn): |x−x0|≤ a, |yj −yj0| ≤ b, j = 1, 2,..., n}

i задовольняють у ньому такi умови:

1) функцiїfj (x, y1, y2,..., yn) неперервнi, а, отже, й обмеженi, тобто |fj (x, y1, y2,...,yn)| ≤ M, j = 1, 2,..., n, M > 0;

2) частиннiпохiднi 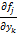, j, k = 1, 2,..., n, iснують та обмеженi. Тодi задача Кошi (2), (4) має єдиний розв’язок принаймнi на вiдрiзку |x − x0| ≤ h, де h = min (a, b/M).

Нехай G – це область простору змiнизмiнних x, y1,..., yn,у кожнiйточцi якої задача Кошi (2), (4) має єдиний розв’язок. Сукупнiсть функцій

yj = ϕj (x, C1, C2,..., Cn), j = 1, 2,..., n, (5) якiвизначенi в деякiйобластiзмiни x, C1, C2,..., Cn i мають неперервнiчастиннiпохiднi за змiнною x, називають загальним розв’язком системи (2) в областi G, якщо:

1) систему (5) можна розв’язати в областi G відносно довiльних сталих C1, C2,..., Cn, тобтоCj = ψj (x, y1, y2,..., yn), j = 1, 2,..., n; (6)

2) для всiх значень (x, y1,..., yn) ∈ G формули (6) визначають такi значення C1, C2,..., Cn, для яких сукупність функцiй (5) є розв’язком системи (2). Розв’язок системи (2), у кожнiйточцi якого виконується умова єдиностi розв’язку задачiКошi, називають частинним. З означення загального розв’язку випливає, що всiрозв’язки, якi утворюються з нього для конкретних значеньдовiльних сталих C1, C2,...,Cn, є частинними. Розв’язок системи, у кожнiйточцi якого порушується умова єдиностi розв’язку задачiКошi для цiєї системи, називають особливим.