Лінійні однорідні диференціальні рівняння n-го порядку зі сталими коефіцієнтами

Розглянемо лінійне диференціальне рівняння n-го порядку

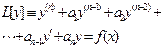, (1)

де коефіцієнти a1, a2,..., An - дійсні числа, а права частина f (x) неперервна на інтервалі(a, b) функція.

Загальне рішення відповідного однорідного рівняння:

L [y] = 0 (2)

Для знаходження загального розв'язку рівняння (1) потрібно знати хоча б одну фундаментальну систему рішень y1 (x), y2 (x),..., yn (x) цього рівняння. Тоді згідно з основною теоремою про рішення однорідного ДР n-го порядку загальним рішенням цього рівняння є y = C1y1 (x) + C2y2 (x) +... + C_ny_n (x),

де C1, C2,..., Cn – довільні сталі.

Спробуємо знайти частинне рішення для однорідного ДУ n-го порядку у вигляді:

y = e^kx (3)

де k -деякий, поки що невизначене число. Підставивши (3) в ліву частину рівняння (1), отримаємо: 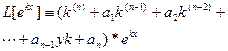(4)

З (4) випливає, що функція (3) буде рішенням ДР (2) тоді і тільки тоді, коли число k є коренем алгебраїчного рівняння

P(k) ≡ kⁿ+ a₁kⁿ⁻¹+ a₂kⁿ⁻²+... + a _n−1 k + a_n = 0. (5)

Многочлен P (k) називають характеристичним многочленом, рівняння (5) - характеристичним рівнянням,яке відповідає рівнянню (2), а його корені - характеристичними числами рівняння (2). Складаючи характеристичне рівняння, потрібно в (2) похідні різних порядків замінити відповідними степенями k. Метод Ейлера. Випадок простих характеристичних чисел. Структура фундаментальної системи рішень, а отже, і загального розв'язку рівняння (2) залежить від характеристичних чисел. Припустимо, що всі характеристичнічисла k1, k2,..., kn дійсні і прості (різні). Тоді згідно (3) функції y₁ = e^k₁^x, y₂ = e^k₂^x,..., y_n = e^k_n^x (6)

є частинними рішеннями рівняння (2). Переконаємося, що вони лінійно незалежними. Для цього обчислимо вронскіан функцій (6): =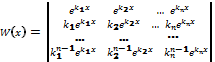

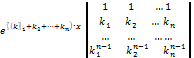
Визначник в правій частині останньої рівності є визначником Вандермонда і, дорівнює добутку всіх множників виду k _j – k_i, где 1≤ i <j≤ n. Імовірно,

k _j ≠ k_i, і тому W (x) ≠ 0Таким чином,функції (6) утворюють фундаментальну систему рішень рівняння (2), а тому функціяy = C₁e^k₁^x+ C₂e^k₂^x+... + C_ne^k_n^x, (7)

ге C1, C2,..., Cn - довільні сталі, є загальним розв'язком рівняння(2).

Теорема 1. Якщо функція y (x) = u (x) + iv (x) явл. рішенням рівняння (2), то кожна з функцій u (x) і v (x) також є вирішенням цього рівняння.