Закон розподілу Максвелла

Теплова (середньоквадратична) швидкість 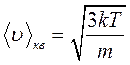являє собою деяку середню характеристику теплового руху всієї сукупності мікрочастинок. Насправді різні частинки рухаються з різними швидкостями, й можна порушити питання про розподіл мікрочастинок за швидкостями. Максвелл теоретично вирішив задачу про розподіл молекул ідеального газу за швидкостями поступального руху в стані теплової рівноваги. Він показав, що ймовірність того, що деяке число молекул 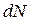із загального числа молекул 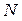має швидкості, що лежать в інтервалі від 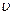до 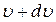, виражається співвідношенням:

(6.12)

де 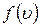– функція розподілу молекул за швидкостями; a 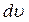– розглянутий інтервал швидкостей.

Вид функції 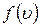можна встановити на прикладі руху молекул ідеального газу в однорідному полі тяжіння. Спочатку вивчимо закон розподілу молекул за значеннями вертикальної складової швидкості 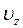. Число молекул зі швидкостями в інтервалі 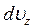, що перебувають у нескінченно тонкому (товщини 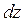) шарі газу на висоті 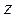(див. рис 6.2), дорівнює:

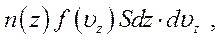де – концентрація молекул газу на висоті .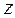

Рухаючись як вільні, ці молекули із часом перейдуть на деяку висоту 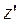, зайнявши шар товщини 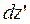. При цьому їхні швидкості будуть перебувати в інтервалі від 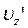до 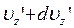. Але це одне й те саме число молекул. Якщо прийняти, що 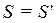, то незмінність числа цих молекул повинна виражатися рівністю:

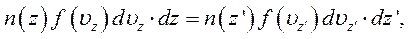
(6.13)

де 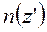– концентрація молекул газу на висоті 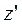. При русі у полі тяжіння горизонтальні складові швидкост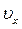і ( і 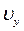) не змінюються, а зміна 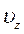визначається законом збереження енергії, відповідно до якого:

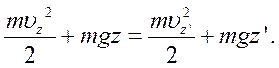(6.14)

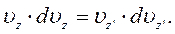Диференціюючи цю рівність при обраних постійних значеннях 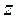та 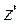, одержуємо:

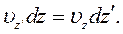За час 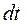молекула на висоті 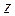пройде шлях 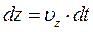, а на висоті 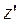– шлях 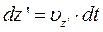. Виключивши звідси 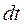, одержимо:

(6.15)

Перемноживши почленно рівняння (6.14) і (6.15), знаходимо:

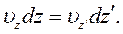З урахуванням останнього рівняння (6.13) спрощується:

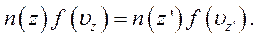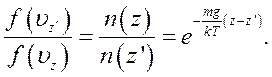Використавши закон розподілу Больцмана у вигляді рівняння (6.7), одержимо:

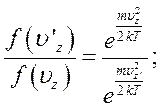На основі закону збереження й перетворення енергій знаходимо:

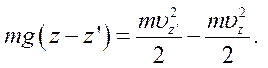Тоді:

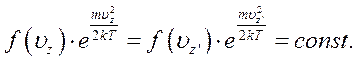Звідси випливає, що:

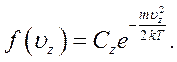(6.16)

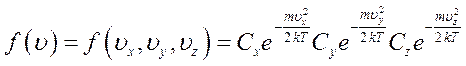У стані теплової рівноваги рух молекул газу рівноймовірний у всіх напрямках. Оскільки ймовірність складної події, що складається із простих незалежних подій, дорівнює добутку ймовірностей цих подій, то повна функція розподілу молекул за швидкостями буде мати вигляд:

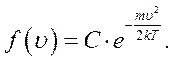Позначивши 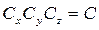и прийнявши, що 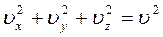одержимо:

(6.17)

На підставі рівнянь (6.12) та (6.17) отримаємо:

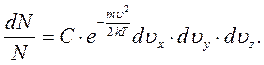(6.18)

Добуток 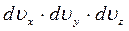являє собою об'єм нескінченно малого паралелепіпеда, побудованого в координатній системі простору швидкостей навколо точки з векторною координатою 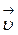. Оскільки тепловий рух молекул газу рівноймовірний у всіх напрямках, то для обчислення 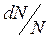необхідно просумувати всі такі елементарні об'єми, що перебувають на відстані 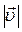. Ці об'єми заповнять кульовий шар між двома нескінченно близькими сферами з радіусами 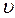та 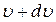. Об'єм такого шару дорівнює 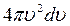. Таким чином, число молекул 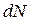зі швидкостями в інтервалі значень між 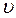та 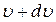дорівнює:

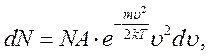(6.19)

де 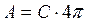– деяка постійна, що не залежить від швидкості молекул. Знайдемо вираження для цієї величини 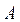. Оскільки в інтервал швидкостей від 0 до 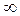ввійдуть всі молекули, то очевидно, що ,

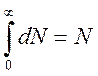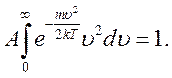
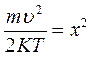Зробивши заміну змінних та скориставшись значенням

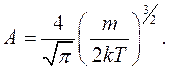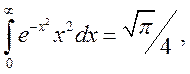знайдемо:

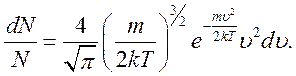З урахуванням цього закон розподілу Максвелла можна записати у вигляді:

(6.20)

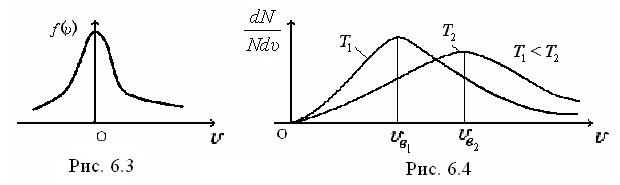
Графік функції (6.20) збігається з гауссовою кривою розподілу випадкової велиини (рис. 6.3), а щільність імовірності розподілу молекул за швидкостями представлена на рис. 6.4.

Як видно з рис. 6.4, при кожній температурі є деяка швидкість 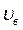, за якої щільність ймовірності максимальна. Цю швидкість називають найбільш імовірною. Дослідивши рівняння (6.19) на екстремум, одержимо:

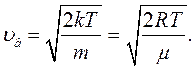(6.21)

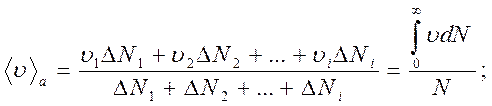
Скориставшись законом розподілу Максвелла, знайдемо середньоарифметичну швидкість молекул:

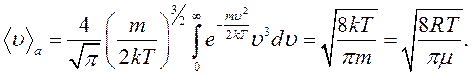Таким чином, стан газу можна охарактеризувати однієї із трьох швидкостей:

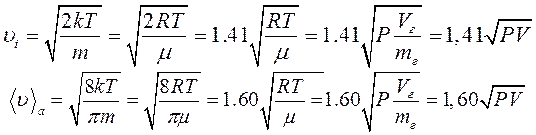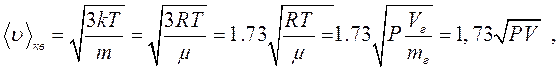де 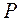, 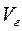та 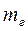– тиск, об'єм і маса газу, 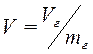– питомий об'єм газу.

Співвідношення між швидкостями має такий вигляд: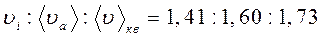

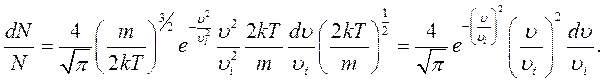Скориставшись рівнянням (6.21), закон розподілу Максвелла (6.20) можна подати через вірогідну швидкість:

Подібно до розподілу Больцмана, розподіл Максвелла, виведений тут для одноатомного ідеального газу, може бути отриманий шляхом більш загальних теоретичних міркувань і має універсальний характер. Однак він отриманий на підставі класичної механіки, і його справедливість обмежена квантовими явищами.

Закон розподілу Максвелла підтверджується різними експериментальними методами, з якими студенти можуть ознайомитися у зазначеному раніше навчальному посібнику [1].