2015-09-06
433
Закон розподілу Больцмана являє собою закон розподілу молекул за потенціальними енергіями, закон розподілу Максвелла – за кінетичними. Очевидно, що об'єднавши ці два закони, можна одержати закон розподілу молекул за повними енергіями. Таке об'єднання можливе на основі теореми про ймовірності складної події.
Згідно з рівнянням (6.9), кількість молекул, що потрапляють у межі об'єму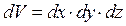 
у точці з координатами 
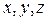, дорівнює:
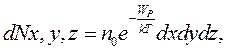
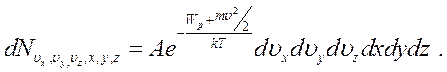де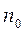 
– число молекул в одиниці об'єму. З урахуванням закону Максвелла число молекул, компоненти швидкості яких лежать у межах від 
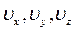до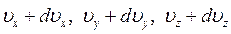 
, а координати в межах від 
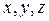до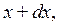 
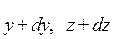буде дорівнювати:
(6.22)
Тут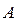 
– нормувальний множник, що дорівнює 
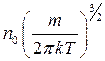. У рівнянні (6.22) потенціальна (
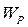) і кінетична (
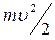) енергії, а отже, і повна енергія 
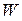можуть набувати безперервного ряду значень. Якщо повна енергія частинки може набувати лише дискретного ряду значень: 
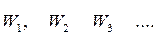(наприклад, внутрішня енергія атома), то розподіл Максвелла–Больцмана має вигляд:
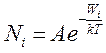
(6.23)
де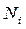 
– число частинок у стані з енергією 
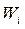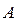, – коефіцієнт пропорційності, що повинен задовольняти умову:
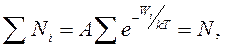
де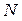 
– загальне число частинок у розглянутій системі. Підставивши це значення 
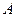у рівняння (6.23), отримаємо остаточний вираз закону розподілу мікрочастинок за дискретними значеннями енергії:
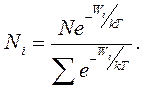(6.24)
