Основные показатели динамики

Для количественной оценки динамики социально-правовых явлений применяются такие статистические показатели, как абсолютные приросты, темпы роста, темпы прироста, которые делятся на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления (например, число осужденных по статьям УК РФ с 1997 г. - года вступления в силу нового Уголовного кодекса). Если сравнение осуществляется при переменной базе и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.

Для рядов динамики со значительными колебаниями уровней в качестве базы сравнения применяются средние уровни.

Абсолютный прирост (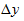) равен разности двух сравниваемых уровней.

Базисный абсолютный прирост

.

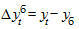Цепной абсолютный прирост

.

Средний абсолютный прирост

,

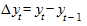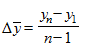где 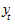- уровень сравниваемого периода; 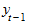- уровень предшествующего периода; 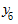- уровень базисного периода; 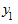, 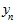- первый и последний уровни ряда соответственно; n - число уровней ряда.

Темп роста (T) - это отношение уровня ряда одного периода к уровню ряда другого периода, выраженное в процентах.

Базисный темп роста .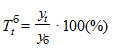

Цепной темп роста .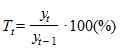

Средний темп роста .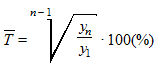

Замечание. Если темп роста и средний темп роста вычисляются в долях (не умножаются на 100%), то они называются соответственно коэффициентом роста и средним коэффициентом роста.

Темп прироста (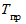) вычисляется как отношение абсолютного прироста (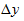) к уровню, принятому за базу сравнения. Темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.

Базисный темп прироста .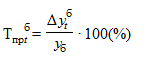

Цепной темп прироста .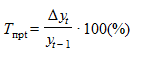

Средний темп прироста .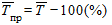

Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:

.

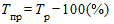Сведем выражения для вычисления указанных выше показателей в таблицу (табл. 17).

Таблица 17