ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА
Цель работы
1.1. Экспериментальное определение моментов инерции твердых тел.
1.2. Проверка теоремы Штейнера.
Теоретическая часть
Момент инерции. Теорема Штейнера
Моментом инерции материальной точки относительно оси называют произведение массы этой точки mi на квадрат ее расстояния до оси 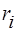

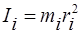 .
.
Моментом инерции тела относительно оси называют сумму моментов инерции материальных точек, из которых состоит это тело
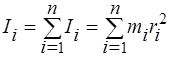 . (2.1)
. (2.1)
Представляя тело состоящим из сколько угодно малых частей объемом dV и массы dm, его момент инерции можно рассчитать интегрированием
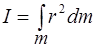 , (2.2)
, (2.2)
где r - расстояние от элемента тела объемом dV до оси, относительно
которой рассчитывается момент инерции.
Так как dm = r dV, где r - плотность тела в данной области dV, то
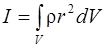 .
.
Если тело однородно, то для всех областей ρ одинаково и
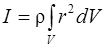 .
.
Наиболее просто определяются моменты инерции тел правильной геометрической формы с равномерным распределением массы по объему.
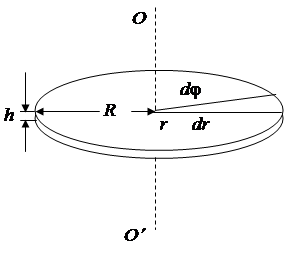
Рассчитаем момент инерции сплошного однородного диска массы m и радиуса R относительно оси симметрии (рис. 2.1).
Выделим элемент тела объемом dV и массы dm, длиной dr, шириной rd jи высотой h, где h - толщина диска отстоящий на расстоянии r от оси OO¢, масса этого элемента dm = r dV = r h dS = r h r d j dr.
Момент инерции диска
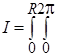 ρr3hdrd j,
ρr3hdrd j,
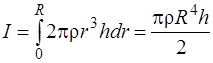
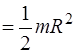 . (2.3)
. (2.3)
| Рис. 2.1 | Из (2.3) следует, что момент инерции сплошного однородного диска зависит только от его массы и радиуса и не зависит от толщины диска. Поэтому формула (2.3) применима для расчета момента инерции сплошного однородного цилиндра относительно оси симметрии. Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции тела относительно |
любой параллельной оси можно определить, воспользовавшись теоремой Штейнера, согласно которой момент инерции I тела относительно произ- вольной оси равен сумме момента инерции тела 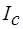 относительно оси,
относительно оси,
параллельной данной и проходящей через центр масс тела, и произведения
массы тела m на квадрат расстояния а между осями
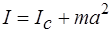 . (2.4)
. (2.4)
 Момент инерции тела относительно оси является мерой инертности тела при вращательном движении (мерой инертности тела при поступательном движении является его масса) и зависит не только от массы тела, но и от ее распределения в пространстве относительно оси. Тело обладает определенным моментом инерции относительно любой оси независимо от того, вращается оно или находится в покое.
Момент инерции тела относительно оси является мерой инертности тела при вращательном движении (мерой инертности тела при поступательном движении является его масса) и зависит не только от массы тела, но и от ее распределения в пространстве относительно оси. Тело обладает определенным моментом инерции относительно любой оси независимо от того, вращается оно или находится в покое.
2.2. Метод трифилярного подвеса
В настоящей работе моменты инерции твердых тел определяются с помощью трифилярного подвеса, представляющего собой диск радиуса R, подвешенный горизонтально на трех нитях длиной L к неподвижному диску меньшего радиуса r (рис. 2.2). Центры дисков расположены на одной вертикальной оси OO¢, вокруг которой нижний диск может совершать крутильные колебания. При колебаниях центр масс С диска радиуса R перемещается вдоль оси OO¢.
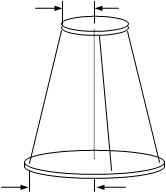 r L C R Рис. 2.2 r L C R Рис. 2.2 | При повороте нижнего диска на угол j вокруг оси OO¢ его перемещение равно h (рис.2.3), а приращение потенциальной энергии Eп=mgh, где m - масса нижнего диска. Колеблющийся диск совершает поступательное и вращательное движение, поэтому его кинетическая |
энергия равна сумме кинетической энергии поступательного движения и кинетической энергии вращательного движения
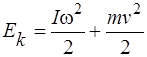 ,
,
где I - момент инерции диска относительно оси OO¢,
w - угловая скорость диска,
v -скорость центра масс диска.
При небольших смещениях диска по вертикали по сравнению с длиной нитей, т.е. при малых углах поворота, пренебрегая вязкостью воздуха, можно показать, что диск совершает гармонические колебания и угол j его поворота изменяется со временем по закону
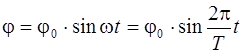 ,
,
где 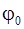 - амплитуда углового смещения,
- амплитуда углового смещения,
T – период колебаний;
а изменение потенциальной энергии диска при максимальном угле поворота 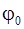 равно максимальной кинетической энергии вращательного движения, которой он обладает в момент прохождения положения равновесия
равно максимальной кинетической энергии вращательного движения, которой он обладает в момент прохождения положения равновесия
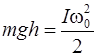 ,
,
где 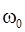 - угловая скорость диска в момент прохождения положения равновесия.
- угловая скорость диска в момент прохождения положения равновесия.
Отсюда момент инерции диска
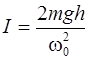 . (2.5)
. (2.5)
Угловая скорость диска меняется по гармоническому закону
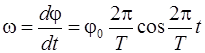 .
.
Следовательно, максимальная угловая скорость 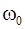 равна
равна
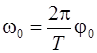 . (2.6)
. (2.6)
Высоту h, на которую поднимается диск, определим из геометрических соображений (рис. 2.3)
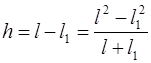 . (2.7)
. (2.7)
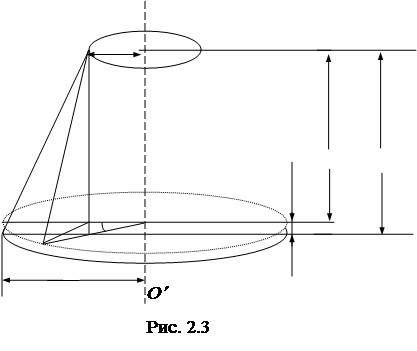 О
О
r
L
l1 l
А
A1 h
R
Но
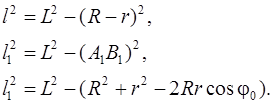 (2.8)
(2.8)
С учетом уравнения (2.8) уравнение (2.7) запишем в виде
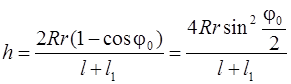 .
.
При малых углах 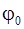
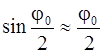 а
а 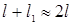 .
.
Таким образом
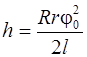 . (2.9)
. (2.9)
Подставляя (2.6) и (2.9) в (2.5) получим
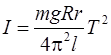 . (2.10)
. (2.10)
Уравнение (2.10) можно применять не только для расчета момента инерции диска (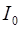 )относительно оси OO¢, но и для расчета момента инерции диска с грузами (I). Момент инерции груза (
)относительно оси OO¢, но и для расчета момента инерции диска с грузами (I). Момент инерции груза (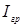 ) можно найти
) можно найти
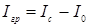 . (2.11)
. (2.11)
 2015-10-16
2015-10-16 1002
1002







