Геометрические характеристики некоторых сечений

Рассмотрим геометрические характеристики наиболее часто встречающихся форм сечений элементов конструкций.

3.4.1. Сечение в форме прямоугольника

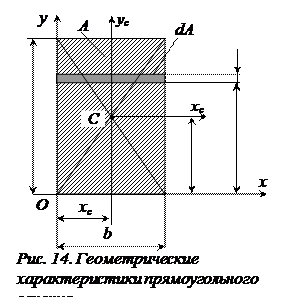Пусть сечение имеет форму прямоугольника со сторонами b x h (рис. 14).

Выберем произвольную систему координат xOy (совместив её со сторонами прямоугольника); выделим на расстоянии у от оси x элементарную площадку dA = b∙dy. Тогда по определению (формула 3.1) получим:

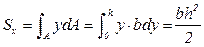. (3.18)

Аналогично определяется статический момент сечения относительно оси y:

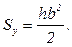(3.19)

Используя формулы (3.2), находим координаты центра тяжести прямоугольника в выбранной системе координат:

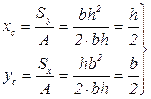, (3.20)

т. е. центр тяжести прямоугольника лежит на пересечении диагоналей.

Для определения осевого момента инерции 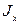сечения относительно оси х воспользуемся формулой (3.6.):

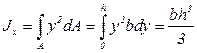. (3.21)

Аналогично находим осевой момент инерции сечения относительно оси у: 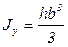. (3.22)

Используя формулы (3.10), найдём осевые моменты инерции прямоугольного сечения относительно центральных осей:

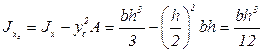. (3.23)

По аналогии находим 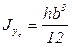. (3.24)

Моменты сопротивления площади сечения данной фигуры найдём, используя формулу (3.14):

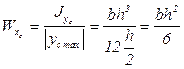; (3.25)

аналогично находим 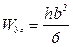. (3.26)

3.4.2. Сечение в форме полукруга и круга

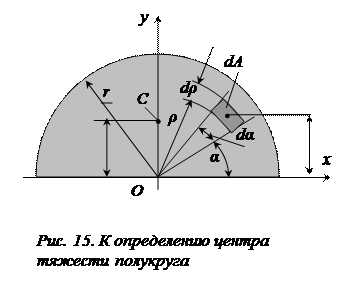
Определим центр тяжести сечения, имеющего форму полукруга с радиусом r (рис. 15). Так как ось y является осью симметрии полукруга, то центр C тяжести сечения лежит на оси y, т. е. x_c = 0.

Для определения ординаты y_c используем выражение (3.1):

,

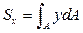где А – площадь полукруга. Из рис. 16 видно, что площадь элементарной площадки

,

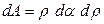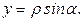
Подставляя значения dA и y в исходную формулу, получим:

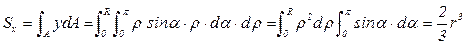. (3.27)

Положение центра тяжести полукруга находим по формуле (3.2):

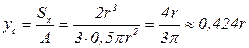. (3.28)

Для определения полярных моментов инерции круглого сечения (рис. 16) выделим из круга элементарное кольцо толщиной 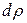радиусом 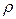и площадью 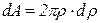. Полярный момент инерции элементарного кольца относительно центра круга С

.

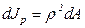Подставляя значение dA и интегрируя, получим

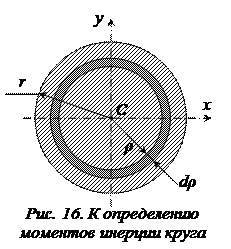
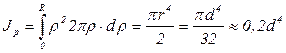. (3.29)

Учитывая (3.9) и (3.17), находим

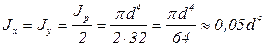. (3.30)

Учитывая (3.14) и (3.16), найдём моменты сопротивления изгибу и кручению сечения круглой формы:

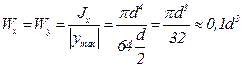; (3.31)

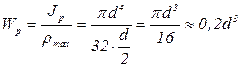. (3.32)

Вопросы для самопроверки

1. Что называется статическим моментом сечения относительно оси? Единица измерения.

2. Чему равен статический момент относительно оси, проходящей через центр тяжести сечения? Центральные оси.

3. Определение координат центра тяжести простого и сложного сечений?

4. Что называется осевым, полярным и центробежным моментом инерции сечения? Единица измерения.

5. Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

6. Связь между осевым и полярным моментами инерции сечения?

7. Осевой момент инерции прямоугольника относительно центральных осей и осей, параллельных его сторонам.

8. Чему равны полярные моменты инерции круга и кольца относительно их центров?

9. Если в плоскости сечения проведён ряд параллельных осей, относительно какой из них осевой момент инерции имеет наименьшее значение?

10. Что представляют собой главные и главные центральные моменты инерции? Чему равен центробежный момент инерции относительно главных осей инерции?

11. Что представляют собой осевой и полярный моменты сопротивления сечения?

Изгиб