Средними величинами в статистических рядах распределения являются мода и медиана, которые относятся к классу структурных (позиционных средних). Их величины зависят лишь от характера частот, то есть от структуры распределения.
Мода – это величина признака (варианта), наиболее часто повторяющаяся в ряду распределения.
Способ вычисления моды зависит от вида ряда распределения.
Для дискретных рядов распределения модой будет значение варианты с наибольшей частотой.
Пример 8. Распределение семей по числу детей в условном регионе характеризуется следующими данными:
| Число детей в семье | ||||||
| Число семей, тыс. |
Требуется определить моду. Просматривая частоты ряда (число семей), замечаем, что наибольшая частота – 25. Эта частота соответствует семьям с одним ребёнком. Таким образом, мода указывает, что в регионе наиболее часто встречаются однодетные семьи.
В интервальном ряду распределения сначала определяется модальный интервал (интервал с наибольшей частотой) и значение моды рассчитывается по формуле
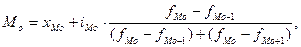
где 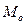 – мода;
– мода;
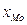 – нижняя граница модального интервала;
– нижняя граница модального интервала;
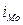 – величина модального интервала (разность между верхней и нижней границами);
– величина модального интервала (разность между верхней и нижней границами);
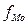 – частота модального интервала;
– частота модального интервала;
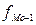 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
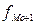 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Рассмотрим пример расчёта моды в интервальном ряду.
Пример 9. Имеются следующие данные о времени посещения кафе быстрого обслуживания:
| Часы работы кафе | 8–10 | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | 20–22 | Итого |
| Число посетителей |
Согласно приведённому условию задачи наибольшее число посетителей (75 чел.) посещают кафе в период с 12 до 14 часов. Следовательно, данный интервал (12–14) является модальным интервалом ряда распределения. Введём следующие обозначения:
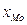 =12;
=12; 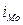 =2;
=2; 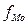 =75;
=75; 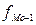 =18;
=18; 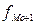 =55.
=55.
Подставим эти значения в формулу моды и произведём вычисления:
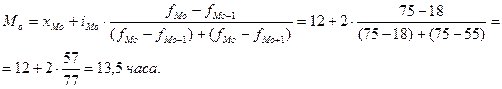
 2015-10-16
2015-10-16 2220
2220








