225
1. Совокупный коэффициент изменяется от 0 до 1.
2. Если R=0 , то z не может быть связана с x и y линейной корреляционной зависимостью, при этом возможна не линейная корреляционная зависимость и даже функциональная зависимость между z,x и y .
3. Если R=1 , то z связана с x и y линейной функциональной зависимостью.
4. Если R отлично от 0 , и от 1 (т.е. от своих крайних значений), то при приближении к 1, теснота линейной связи z с x и y увеличивается.
Таким образом совокупный коэффициент- есть мера тесноты линейной корреляционной зависимости между z,x, y . На практике часто важно оценить влияние на z отдельно x ,и отдельно y .Это осуществляется с помощью частных коэффициентов корреляции. Частный коэффициент корреляции между z и x обозначается как
.
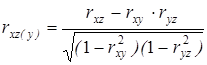С его помощью оценивается теснота линейной корреляционной зависимости между z и x , когда y -остается постоянной. Теснота линейной корреляционной зависимости между z и y, когда x -постоянная, оценивается с помощью частного коэффициента корреляции между y и z .
;
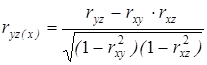каждый из выше рассмотренных частных коэффициентов изменяется от -1 до 1. Когда коэффициент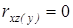 
, то исключается линейная корреляционная зависимость x и z , не линейная корреляционная зависимость и даже функциональная зависимость между x и z остаются возможными . Если этот коэффициент равен 1, то зависимость - линейно- функциональная.
