Методические указания

Часть

Общее уравнение плоскости в пространстве записывается в виде

.

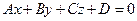При этом А, В, С не равны одновременно нулю, т.е. .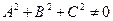

Если даны две плоскост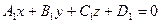и и ,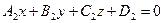

Условием их параллельности является пропорциональность коэффициентов при одноименных переменных, т.е

,

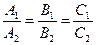а условием из перпендикулярности

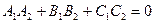
Виды прямой в пространстве:

1. Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе уравнений

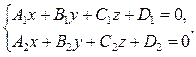
2. Если прямая параллельна вектору 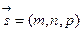и проходит через точку 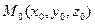, то ее уравнения могут быть получены из условия параллельности вектора 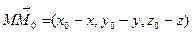, где 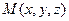- текущая точка на прямой, и вектора 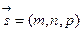, т.е.

.

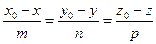Эти уравнения называются каноническими уравнениями прямой в про странстве.

Уравнение плоскости через три точки.

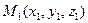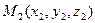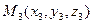, , в декартовой системе координат, не лежащие на одной прямой.

Уравнение имеет вид

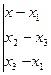
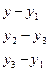
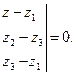
5. Рекомендуемое содержание отчета (для студента).

1. Название лабораторной работы.

2. Цель и задачи исследований.

3. Электронно-вычислительные средства для расчетов.

4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).

5. Выводы.

6. Анализ и защита лабораторной работы производится по результатам представленного студентами отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы, выполненные групповые задания).

Преподаватель оценивает знание каждого студента.

Литература