Для указанных отображений найти образ 1, прообраз 1 и определить тип отображения.
1. 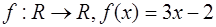
Ответ: 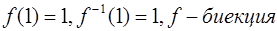 ;
;
2. 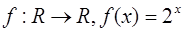
Ответ: 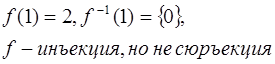 ;
;
3. 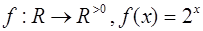
Ответ: 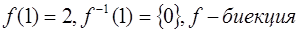 ;
;
4. 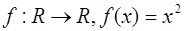
Ответ: 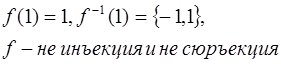 ;
;
5. 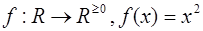
Ответ: 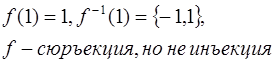 ;
;
6. 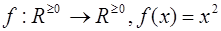
Ответ: 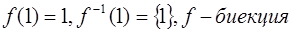 ;
;
7. 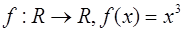
Ответ: 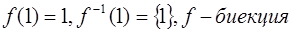 ;
;
8. 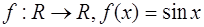
Ответ: 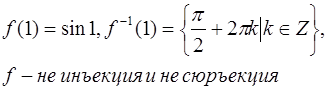 ;
;
9. 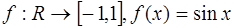
Ответ: 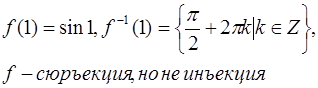 ;
;
10. 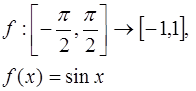
Ответ: 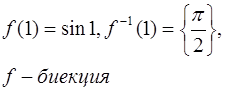 ;
;
11. 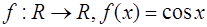
Ответ: 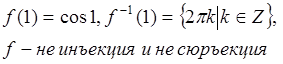 ;
;
12. 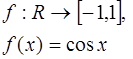
Ответ: 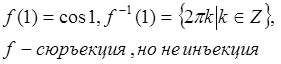 .
.
Если заданы преобразования 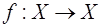 и
и 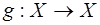 , то преобразование
, то преобразование 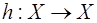 , являющееся результатом последовательного выполнения сначала преобразования
, являющееся результатом последовательного выполнения сначала преобразования 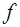 , а затем и преобразования
, а затем и преобразования 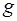 , называется произведением преобразований
, называется произведением преобразований 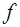 и
и 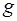 :
: 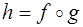 .
.
Для преобразований 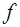 ,
, 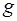 и
и 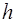 одного и того же множества
одного и того же множества 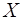 справедливы следующие законы:
справедливы следующие законы:
· 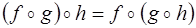 ;
;
· 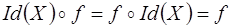 ;
;
· 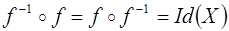 .
.
Задача 6.
Найти 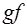 ,
, 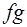 ,
, 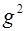 ,
, 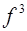 , если
, если
1) 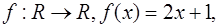
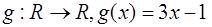
Ответ: 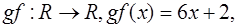
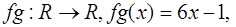
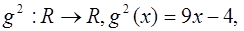
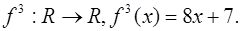
2) 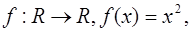
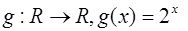
Ответ: 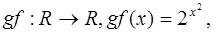
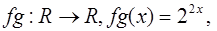
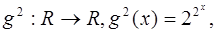
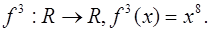
Практическое занятие 2. Комплексные числа
Вопросы для повторения
1. Понятие комплексного числа.
2. Понятие мнимой единицы (числа 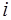 ).
).
3. Основные операции над комплексными числами.
4. Представление комплексного числа в тригонометрической форме.
5. Понятие модуля комплексного числа.
6. Понятие аргумента комплексного числа.
7. Умножение и деление комплексных чисел в тригонометрической форме.
8. Формула Муавра.
Множеством комплексных чисел называется множество 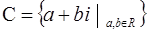 , которое представляет собой множество всех двучленов вида
, которое представляет собой множество всех двучленов вида 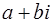 .
.
Мнимой единицей 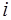 называется корень уравнения
называется корень уравнения 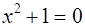 или
или 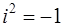 .
.
Действительное число 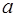 называется действительной частью комплексного числа
называется действительной частью комплексного числа 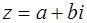 ,
, 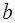 ‑ мнимой частью или коэффициентом при мнимой единице.
‑ мнимой частью или коэффициентом при мнимой единице.
Число 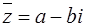 называется сопряженным числу
называется сопряженным числу 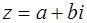 .
.
Расстояние от точки 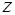 до начала координат есть действительное неотрицательное число
до начала координат есть действительное неотрицательное число 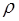 , которое называется модулем комплексного числа
, которое называется модулем комплексного числа 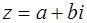 и находится по формуле
и находится по формуле 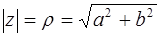 .
.
Угол между положительным направлением действительной оси и радиус-вектором точки 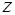 называется аргументом
называется аргументом 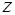 и определяется из равенств
и определяется из равенств 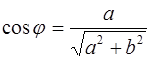 ,
, 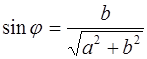 . Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных
. Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных 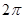 , при этом положительные углы отсчитываются против часовой стрелки.
, при этом положительные углы отсчитываются против часовой стрелки.
Тригонометрической формой комплексного числа 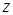 называется запись числа в виде:
называется запись числа в виде:
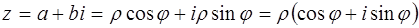 .
.
Показательной формой комплексного числа 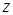 называется запись числа в виде
называется запись числа в виде 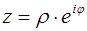 .
.
Формула возведения комплексного числа в степень 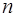 (формула Муавра):
(формула Муавра):
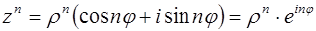 .
.
Формула вычисления корней степени 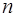 комплексного числа
комплексного числа 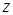 :
:
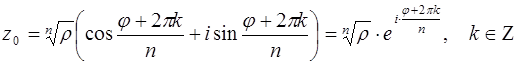 .
.
 2015-10-13
2015-10-13 360
360








