Этот критерий, позволяющий судить об устойчивости САР по частотным характеристикам разомкнутой системы (амплитудно-фазовой или логарифмическим), нашел наибольшее распространение, поскольку позволяет использовать не только аналитически построенные частотные характеристики, но и найденные экспериментально.
Критерий был предложен Найквистом в 1932 г. для анализа электронных усилителей с обратной связью. В 1938 г. был обобщен и применен А. В. Михайловым для анализа САР.
Пусть передаточная функция разомкнутой системы 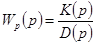 , причем из физических соображений следует, что степень М полинома
, причем из физических соображений следует, что степень М полинома 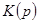 не выше степени N полинома
не выше степени N полинома 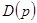 . Образуем функцию Найквиста
. Образуем функцию Найквиста
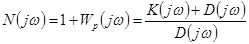 (5-12)
(5-12)
и рассмотрим изменение ее аргумента при изменении ω от 0 до 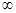 , которое обозначим
, которое обозначим 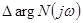 . Обратим внимание, что
. Обратим внимание, что 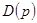 является характеристическим полиномом разомкнутой системы, а
является характеристическим полиномом разомкнутой системы, а 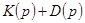 - характеристическим полиномом замкнутой системы, при этом степени обоих характеристических полиномов равны N.
- характеристическим полиномом замкнутой системы, при этом степени обоих характеристических полиномов равны N.
Рассмотрим три возможных случая, когда разомкнутая система устойчива, неустойчива и нейтральна.
1-й случай — система в разомкнутом состоянии устойчива.
Будет ли она устойчива при замыкании и при каких условиях?
Рассмотрим изменение аргумента функций 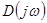 и
и 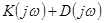 .
.
Полином 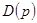 можно представить в виде
можно представить в виде
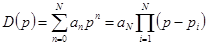
где 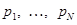 — корни характеристического уравнения
— корни характеристического уравнения 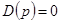 .
.
Тогда
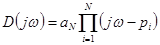 и
и 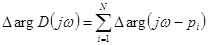
Рассмотрим геометрическое представление комплексного числа 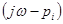 в виде вектора при фиксированном значении ω (рис. 5-3). Начало вектора
в виде вектора при фиксированном значении ω (рис. 5-3). Начало вектора 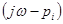 лежит в точке
лежит в точке
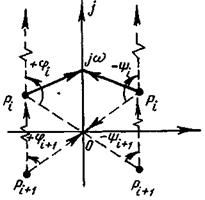
Рис. 5-3. К выводу критерия Найквиста
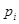 , а конец — на мнимой оси в точке
, а конец — на мнимой оси в точке 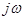 . Поэтому при
. Поэтому при 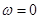 конец вектора лежит в начале координат, а при
конец вектора лежит в начале координат, а при 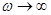 — в бесконечно далекой точке на мнимой оси. При изменении
— в бесконечно далекой точке на мнимой оси. При изменении 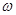 от 0 до
от 0 до 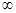 вектор
вектор 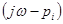 повернется в положительном направлении на угол
повернется в положительном направлении на угол 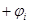 , а вектор
, а вектор 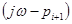 на угол
на угол 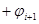 . Очевидно, что
. Очевидно, что 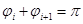 .Таким образом, один левый корень дает изменение аргумента функции
.Таким образом, один левый корень дает изменение аргумента функции 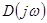 на
на 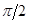 , а пара комплексно-сопряженных левых корней — на π. Вследствие этого
, а пара комплексно-сопряженных левых корней — на π. Вследствие этого
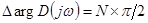 ,
,
поскольку разомкнутая система устойчива (все корни  — левые).
— левые).
Если потребовать, чтобы и замкнутая система была
устойчива (чтобы все корни  были левыми), необходимо, рассуждая аналогично,
были левыми), необходимо, рассуждая аналогично,
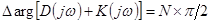
Но в этом случае изменение аргумента функции Найквиста
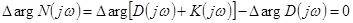 . (5-13)
. (5-13)
Поскольку функция Найквиста — это АФХ разомкнутой системы, смещенная вправо на единицу, то можно рассматривать изменение аргумента не функции Найквиста относительно начала координат, а изменение аргумента (фазу) АФХ относительно точки 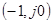 . Поэтому условие устойчивости (5-13) можно сформулировать так: замкнутая система устойчива, если АФХ разомкнутой системы не охватывает точку
. Поэтому условие устойчивости (5-13) можно сформулировать так: замкнутая система устойчива, если АФХ разомкнутой системы не охватывает точку 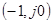 .
.
Пример 5-2. Определим предельный коэффициент САР, рассмотренной в примере 5-1. Амплитудно-фазовые характеристики данной системы при разных значениях k показаны на рис. 5-4. Согласно критерию Найквиста при k 1
САР устойчива, а при k 2 — неустойчива (изменение аргумента 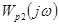 относительно точки
относительно точки 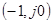 равно π). Если
равно π). Если 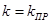 , то АФХ проходит через точку
, то АФХ проходит через точку 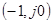 , т. е.
, т. е.
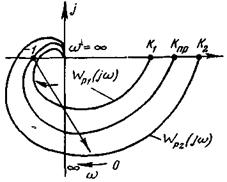
Рис. 5-4 К определению предельного коэффициента усиления САР
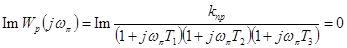 ,
,
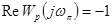 .
.
Решая эти уравнения относительно  и
и  (частота, на которой фазовый сдвиг равен
(частота, на которой фазовый сдвиг равен 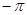 ), получаем
), получаем
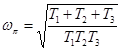 ,
,
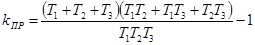 ,
,
что совпадает с полученным ранее выражением (5-11).
2-й случай — система в разомкнутом состоянии неустойчива.
Если система неустойчива в разомкнутом состоянии (это может случиться при рассмотрении многоконтурных систем или одноконтурных с неустойчивыми звеньями), то ее характеристическое уравнение 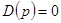 имеет правые корни. Если обозначить их число т, то,
имеет правые корни. Если обозначить их число т, то,
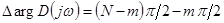 ,
,
поскольку каждый правый корень дает отрицательное изменение аргумента (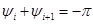 ) (см. рис. 5-3).
) (см. рис. 5-3).
Потребуем, чтобы замкнутая система была устойчива, тогда необходимо, чтобы
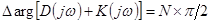
Но в этом случае
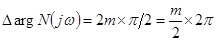 . (5-14)
. (5-14)
Таким образом, замкнутая система устойчива, если АФХ разомкнутой системы охватывает 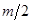 раз в положительном направлении точку
раз в положительном направлении точку 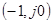 . Эта формулировка обобщает формулировку первого случая для
. Эта формулировка обобщает формулировку первого случая для 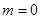 .
.
Пример 5-3. На рис. 5-5 показана АФХ разомкнутой системы, имеющей
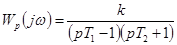 .
.
При 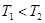 АФХ проходит в четвертом квадранте (характеристика 3), а при
АФХ проходит в четвертом квадранте (характеристика 3), а при 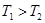 — в третьем квадранте (характеристики 1, 2). Поскольку в данном случае характеристическое уравнение разомкнутой системы
— в третьем квадранте (характеристики 1, 2). Поскольку в данном случае характеристическое уравнение разомкнутой системы  имеет один правый корень
имеет один правый корень 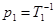 , то для устойчивости замкнутой системы надо, чтобы АФХ охватывала точку
, то для устойчивости замкнутой системы надо, чтобы АФХ охватывала точку 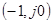 «половину раза», т. е. изменение ее аргумента относительно этой точки должно быть равно
«половину раза», т. е. изменение ее аргумента относительно этой точки должно быть равно 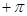 . Этому удовлетворяет только характеристика 2
. Этому удовлетворяет только характеристика 2
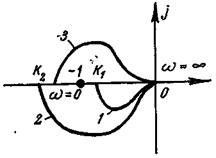
Рис. 5-5. АФХ разомкнутой неустойчивой системы
(для характеристики 3 изменение аргумента равно 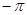 ).
).
Таким образом, устойчивость САР обеспечивается при двух условиях: 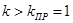 и
и 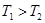 .
.
3-й случай — система, в разомкнутом состоянии нейтральна.
В этом случае передаточная функция системы в разомкнутом состоянии имеет вид
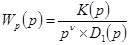 , (5-15)
, (5-15)
где 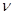 — число интегрирующих звеньев в системе.
— число интегрирующих звеньев в системе.
Из (5-15) следует, что АФХ при 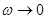 уходит в бесконечность (имеет разомкнутый вид), а поэтому трудно судить о ходе АФХ на малых частотах. Рассмотрим «дополненную АФХ»
уходит в бесконечность (имеет разомкнутый вид), а поэтому трудно судить о ходе АФХ на малых частотах. Рассмотрим «дополненную АФХ»
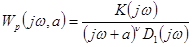 , (5-16)
, (5-16)
которая переходит в исходную при 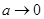 . Если построить «дополненную АФХ» при конечном
. Если построить «дополненную АФХ» при конечном 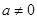 вид ее при малых частотах показан пунктиром, а при больших частотах она практически совпадает с исходной. Введение параметра а сводит 3-й случай к двум первым, а «дополнение в бесконечности» (так называют пунктирное дополнение на рис. 5-6, петля которого уходит в бесконечность при
вид ее при малых частотах показан пунктиром, а при больших частотах она практически совпадает с исходной. Введение параметра а сводит 3-й случай к двум первым, а «дополнение в бесконечности» (так называют пунктирное дополнение на рис. 5-6, петля которого уходит в бесконечность при 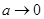 придает АФХ нейтральной системы замкнутый вид, по которому можно судить об изменении ее аргумента относительно точки
придает АФХ нейтральной системы замкнутый вид, по которому можно судить об изменении ее аргумента относительно точки 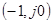 . «Дополнение в бесконечности» обычно проводят мысленно, проводя пунктирную линию от некоторой точки на положительной полуоси до встречи с действительной АФХ, проходя по направлению движения часовой стрелки
. «Дополнение в бесконечности» обычно проводят мысленно, проводя пунктирную линию от некоторой точки на положительной полуоси до встречи с действительной АФХ, проходя по направлению движения часовой стрелки  квадрантов.
квадрантов.
Формулировка критерия Найквиста практически не отличается от данных ранее: замкнутая система устойчива, если АФХ разомкнутой системы с «дополнением в бесконечности» охватывает точку 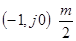 — раз, где т — число правых корней уравнения
— раз, где т — число правых корней уравнения 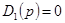 .
.
Пример 5-4. Рассмотрим систему с астатизмом 2-го по рядка, когда
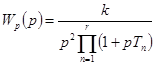 . (5-17)
. (5-17)
АФХ разомкнутой системы для r= 2, 3 показаны на рис. 5-7, где пунктиром построено «дополнение в бесконечности». Согласно критерию, Найквиста эта система неустойчива при замыкании при любых k, Тп, r= 1,2,.... Системы такого типа называют структурно-неустойчивыми. Для получения устойчивой системы с астатизмом 2-го порядка следует провести коррекцию и добиться, чтобы ее АФХ на частотах в районе точки  имела вид кривой 3, которая уже не охватывает эту точку.
имела вид кривой 3, которая уже не охватывает эту точку.
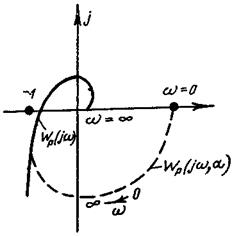
Рис. 5-6. Построение АФХ нейтральной разомкнутой системы
Этого можно добиться, например, вводя в систему звенья, дающие опережение по фазе на указанных частотах (например, упругие — дифференцирующие звенья).
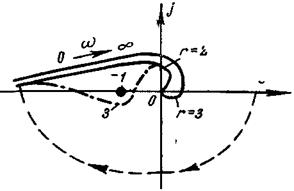
Рис. 5-7 Примеры АФХ структурно-неустойчивых систем
Критерий Найквиста легко можно применить к логарифмическим характеристикам разомкнутой системы. Рассмотрим это на примере разомкнутой системы, имеющей АФХ, изображенную на рис. 5-8 ,а. Соответствующие ей логарифмические характеристики 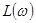 и
и 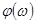 показаны на рис. 5-8, б. Назовем переход амплитудно-фазовой характеристикой отрезка
показаны на рис. 5-8, б. Назовем переход амплитудно-фазовой характеристикой отрезка  положительным, если он совершается сверху вниз при возрастании частоты (на частоте
положительным, если он совершается сверху вниз при возрастании частоты (на частоте  ), и
), и
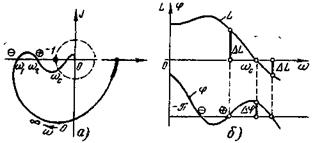
Рис 5-8 К формулировке критерия Найквиста для логарифмических частотных характеристик
отрицательным, если он совершается снизу вверх (на частоте 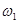 ). Этим переходам на логарифмических характеристиках соответствуют точки пересечения характеристикой
). Этим переходам на логарифмических характеристиках соответствуют точки пересечения характеристикой 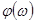 уровней
уровней 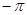 ,
, 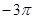 ,... в том диапазоне частот, где
,... в том диапазоне частот, где 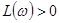 . Поэтому критерий устойчивости можно сформулировать так: САР устойчива, если разность между числами положительных и отрицательных переходов логарифмической характеристики равна
. Поэтому критерий устойчивости можно сформулировать так: САР устойчива, если разность между числами положительных и отрицательных переходов логарифмической характеристики равна 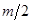 , где т — число правых корней характеристического уравнения разомкнутой системы. При m =0 (система устойчива или нейтральна в разомкнутом состоянии) эта разность должна быть равна нулю.
, где т — число правых корней характеристического уравнения разомкнутой системы. При m =0 (система устойчива или нейтральна в разомкнутом состоянии) эта разность должна быть равна нулю.
При анализе устойчивости обычно оценивают запас устойчивости, т. е. степень удаленности системы от границы устойчивости. Для обеспечения запаса устойчивости необходимо, чтобы АФХ проходила в достаточной удаленности от «опасной» точки 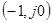 . Различают:
. Различают:
1) запас устойчивости по фазе 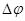 — величина фазы АФХ, на которую должна уменьшиться фаза на частоте среза
— величина фазы АФХ, на которую должна уменьшиться фаза на частоте среза 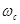 , чтобы система оказалась на границе устойчивости;
, чтобы система оказалась на границе устойчивости;
2) запас по амплитуде 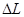 , — величина допустимого
, — величина допустимого
подъема (опускания) ЛАЧХ, при которой система окажется на границе устойчивости.
При проектировании САР рекомендуется выбирать 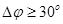 ,
, 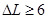 дб. Последнее соответствует примерно двойному запасу коэффициента усиления, т. е. действительный коэффициент усиления примерно в два раза меньше предельного.
дб. Последнее соответствует примерно двойному запасу коэффициента усиления, т. е. действительный коэффициент усиления примерно в два раза меньше предельного.
Глава 6
КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ
Устойчивость является необходимым, но не достаточным условием применимости САР. Необходимо также, чтобы САР имела требуемое качество процессов регулирования, которое оценивают по некоторым показателям процесса регулирования в различных типовых режимах: в режиме покоя (статическом), в режиме отработки ступенчатых управляющих и возмущающих воздействий, в режиме линейно-нарастающих во времени или гармонических воздействий и т. д. Естественно, что наиболее важны показатели качества для того режима, который наиболее характерен для данной конкретной САР. Так, для систем стабилизации весьма важны показатели в статическом режиме, для позиционных следящих систем и систем программного регулирования — в режиме отработки ступенчатых воздействий, а, например, для системы стабилизации корабля на качке — в режиме гармонического воздействия и т. д.
Говорят, что САР имеет заданное качество, если обеспечиваются следующие показатели:
1) заданная точность, характеризуемая ошибками в типовых режимах;
2) заданное быстродействие, характеризуемое временем протекания переходных процессов в системе;
3) заданный запас устойчивости, характеризуемый склонностью системы к колебаниям.
§ 6-1. Точность регулирования
Точность САР характеризуют ошибкой е (рис. 6-1) в установившемся режиме. Для ее определения пользуются теоремой о конечном значении
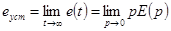 , (6-1)
, (6-1)
где Е(р) — изображение ошибки по Лапласу.
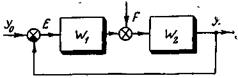
Рис. 6-1.
Если на линейную систему действует несколько воздействий, то ошибка, как это следует из принципа суперпозиции, содержит в общем случае столько же составляющих, каждая из которых обусловлена только своим воздействием при нулевых других. Так, например, для системы рис. 6-1, где имеется два воздействия: задающее (уставка) 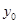 и возмущающее f, ошибка имеет две составляющих
и возмущающее f, ошибка имеет две составляющих
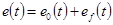 ,
,
где е 0показывает ошибку воспроизведения воздействия у 0, я еf обусловлена действием возмущения f.
Изображения по Лапласу для них легко найти по принципу суперпозиции
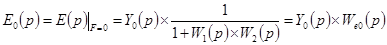 , (6-2а)
, (6-2а)
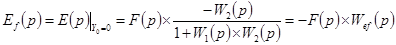 , (6-26)
, (6-26)
где 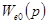 ,
, 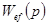 — передаточные функции системы относительно ошибки соответственно по задающему и возмущающему воздействиям.
— передаточные функции системы относительно ошибки соответственно по задающему и возмущающему воздействиям.
В зависимости от характера воздействий в системе могут быть различные установившиеся режимы:
1) при постоянных во времени воздействиях — статический режим;
2) при линейно-нарастающих во времени воздействиях — кинетический режим;
3) при произвольно изменяющихся воздействиях — динамический режим.
Установившиеся ошибки в таких режимах носят соответствующие названия, при этом часто указывают, о какой составляющей ошибки идет речь.
1а. Статическая ошибка по задающему воздействию находится из (6-2а) с помощью (6-1) при 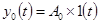
Тогда
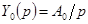
и
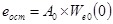 . (6-3)
. (6-3)
Если 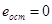 , то систему называют астатической по отношению к задающему воздействию, в противном случае — статической. Как видно из (6-3), статическая ошибка по уставке отсутствует
, то систему называют астатической по отношению к задающему воздействию, в противном случае — статической. Как видно из (6-3), статическая ошибка по уставке отсутствует
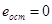 при
при 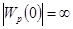 , (6-4а)
, (6-4а)
т. е. когда передаточная функция разомкнутой системы имеет вид
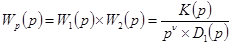 , (6-4б)
, (6-4б)
где 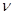 — порядок астатизма системы;
— порядок астатизма системы;
К 1, D 1 — полиномы от р, имеющие нулевую младшую степень р.
Как видно из (6-4), астатизм системы зависит от наличия в ней интегрирующих звеньев.
1б. Статическая ошибка по возмущению находится из (6-2б) с помощью (6-1) при 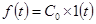 . Тогда
. Тогда
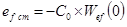 . (6-5)
. (6-5)
Легко указать условие отсутствия статической ошибки по возмущению:
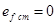 при
при 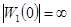 (6-6)
(6-6)
В самом деле, перепишем (6-5) в виде
 .
.
но 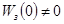 ,
,
где 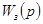 — передаточная функция замкнутой системы;
— передаточная функция замкнутой системы;
 — передаточная функция части системы между точками приложения возмущения и измерения ошибки.
— передаточная функция части системы между точками приложения возмущения и измерения ошибки.
Условие (6-6) требует наличия в указанной части системы интегрирующих звеньев (см. (6-4)).
2. Кинетическая ошибка по задающему воздействию находится из (6-2а) с помощью (6-1) при
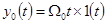
где 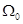 — скорость воздействия.
— скорость воздействия.
Тогда
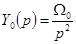
и
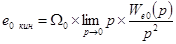 . (6-7)
. (6-7)
Если система имеет астатизм 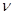 -го порядка и ее передаточная функция имеет вид
-го порядка и ее передаточная функция имеет вид
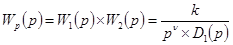 , (6-8)
, (6-8)
то из (6-7) получаем
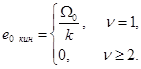 (6-9)
(6-9)
В следящих системах величину k в (6-8) называют добротностью. Как видно из (6-9), кинетическая ошибка следящей системы тем меньше, чем больше ее добротность.
Аналогично (6-7) можно получить из (6-2б) выражение для кинетической ошибки по возмущению.
3. Динамическая ошибка обычно рассматривается для случая, когда воздействия являются гармоническими.
Если 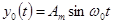 , то амплитуда установившейся гармонической ошибки по задающему воздействию равна
, то амплитуда установившейся гармонической ошибки по задающему воздействию равна
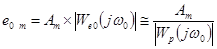 . (6-10а),
. (6-10а),
Аналогично можно найти динамическую ошибку по возмущению: если 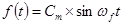 , то из (6-2б)получаем амплитуду установившейся ошибки по возмущению
, то из (6-2б)получаем амплитуду установившейся ошибки по возмущению
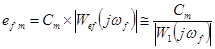 . (6-10б)
. (6-10б)
Пример 6-1. Рассмотрим САР скорости двигателя, (см. рис. 1-7). Для данной системы стабилизации характерен статический режим работы. Найдем ее статическую ошибку.
Структурная схема статической САР (рис. 1-7,а) дана на рис. 4-17,б, где 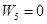 . Передаточная функция по ошибке относительно задающего воздействия равна
. Передаточная функция по ошибке относительно задающего воздействия равна
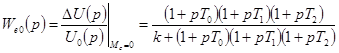 ,
,
где 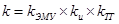 ; передаточная функция по ошибке относительно возмущения — момента сопротивления нагрузки — равна
; передаточная функция по ошибке относительно возмущения — момента сопротивления нагрузки — равна
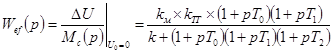
Таким образом,
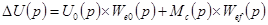 .
.
При постоянных значениях
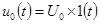 ,
, 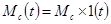
получаем по теореме о конечном значении (6-1)
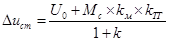
что дает при пересчете на скорость статическую ошибку
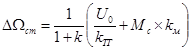 .
.
Пример 6-2. Рассмотрим следящую систему (рис. 1-10). Найдем ее статическую и кинетическую ошибки по отношению к задающему воздействию 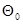 .
.
Передаточная функция исходной разомкнутой системы (рис. 6-2)
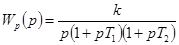 ,
,
где k — добротность системы, 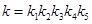 ,
, 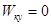 .
.
Как следует из (6-4), статическая ошибка отсутствует. На практике наличие статической ошибки, главным образом, объясняется наличием трения в серводвигателе, приводящем к появлению зоны нечувствительности.
Кинетическая ошибка при 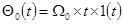 равна (см. (6-9))
равна (см. (6-9))
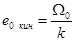
Если следящая система стабилизируется тахометрической обратной связью (см. рис. 6-2), то передаточная функция разомкнутой системы с коррекцией (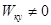 )
)
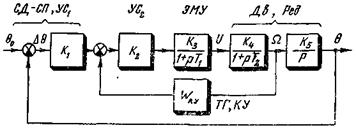
Рис. 6-2
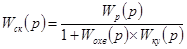 ,
,
где
 .
.
Если применяется жесткая обратная связь, когда 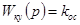 , то кинетическая ошибка равна
, то кинетическая ошибка равна
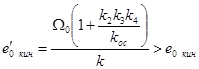
 2015-10-13
2015-10-13 3727
3727
